Упорядоченная -выборка, в которой элементы могут повторяться, называется -размещением с повторениями. Иными словами, размещениями с повторениями из n элемен­тов по k называют векторы длины k, составленные из n элементов множества X.

Число размещений с повторениями из n элементов по k опре­деляется оценкой соответствующего декартова произведения n-элементного множества , обозначается (от ан­глийского слова Assing – назначать) и вычисляется следующим образом:

.

Таким образом, первый элемент вектора длины k выбирается n способами, второй также n способами и т.д.: .

Пример 1

Сколькими способами можно оснастить две различные фирмы компьютерами трех типов?

Каждый способ оснащения есть выборка (3,2), т.е. вектор длины 2, составленный из трехэлементного множества типа Т = {t₁, t₂, t₃}. Поэтому число способов оснащения – число размещений с повторениями из 3 по 2:

.

Рассмотрим этот пример подробнее:

.

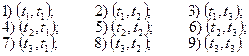Получили различные упорядочения двухэлементных векторов из трех элементного множества, т.е. множество Т².

Здесь каждый вектор соответствует способу оснащения. Видно, что, например,  считаются разными способами, так как фирмы предполагаются различными («первая – первым типом», «вторая – вторым» и т.д.). Имеются повторения:

.

В ряде задач необходимо определить число векторов длины k из n элементов данного множества без повторения элементов.

Если элементы упорядоченной -выборки попарно раз­личны, то они называются -размещением без повторений или просто -размещением.

Число таких размещений без повторений обозначается.

Каждое -размещение без повторения является упорядо­ченной последовательностью длины k, элементы которой попар­но различны и выбираются из множества с n элементами. Тогда первый элемент этой последовательности может быть выбран n способами, после каждого выбора первого элемента последова­тельности второй элемент может быть выбран n-1 способами и т.д., k-й элемент выбирается n-(k-1) способами. Таким образом:

.

Здесь  – факториал натурального числа p. Под факториалом  понимают произведение всех натуральных чисел от 1 до p, т.е.:

.

Например:

.

Считают, что .

При

.

Очевидно, что при

.

Пример 2

Сколькими способами можно скомплектовать груп­пу из трех студентов для прополки клубники в составе начальни­ка и подчиненных?

Речь идет о выборе упорядоченных двухэлементных подмно­жеств множества студентов, состоящего из трех элементов (К = {1, 2, 3}), т.е. о размещениях без повторений из трех элемен­тов по 2. Поэтому число способов комплектования групп студентов равно:

Подробнее наше множество можно записать в виде векторов из номеров студентов (например, по журнальному списку) первая компонента которого обознача­ет номер студента-начальника, вторая – подчиненного:

(1,2), (1,3), (2,1), (2,3), (3,1), (3,2).

Ясно, что здесь существенен порядок следования компонен­тов и не может быть повторений (один студент не может быть начальником и подчиненным одновременно), поэтому это мно­жество – подмножество декартового произведения.

Пример 3

Сколькими способами можно провести распределе­ние 10 механизаторов по трем сушильным установкам? Один механизатор назначается на одну сушильную установку.

Распределение механизаторов – размещение без повторений из 10 элементов по 3, поэтому получим: