Рассмотрим различные упорядочения n-элементного множе­ства X (вектора длины n, составленные из n-элементного множе­ства). В отличие от декартова произведения полученные при этом векторы отличаются лишь порядком следования элементов и называются перестановками без повторений из п элементов. Число перестановок без повторений из n элементов обозначается .

К перестановкам без повторений можно прийти, полагая, что осуществляется размещение без повторений из n элементов по n:

.

Пример 1

Сколько существует возможных последовательнос­тей выполнения проверок финансовой деятельности трех подраз­делений?

Требуется получить число перестановок без повторений из трех элементов, т.е.

Р₃ = 3! = 6.

Получим все эти последовательности:

(1,2,3), (1,3,2), (2,3,1), (2,1,3), (3,1,2), (3,2,1).

Пример 2

Сколько можно составить пятизначных шифров-чи­сел, не кратных 5, из цифр 1, 2, 3, 4, 5 без повторений цифр?

Всего из пяти цифр можно составить Р₅ = 5! = 120 пятизнач­ных шифров-чисел, но они будут включать и кратные 5.

Сколько будет шифров, кратных 5?

Из данного набора чисел кратными 5 могут быть числа, содержащие 5 в младшем разряде. Если циф­ру 5 записать в младшем разряде, то остальные цифры 1, 2, 3, 4 можно распределить по разрядам Р₄= 4! = 24 способами. Таким образом, число пятизначных шифров из чисел 1,2, 3, 4, 5 без пов­торения чисел и не кратных 5 будет:

120 – 24 = 96.

Перестановки без повторений можно интерпретировать как различные варианты векторов, состоящих из неповторяющихся компонентов, которые получаются перестановкой компонентов.

По аналогии при наличии одинаковых компонентов в неко­тором векторе получаем задачу оценки так называемых переста­новок с повторениями данного состава. Рассмотрим вначале пример.

Пример 3

Определим, сколько различных последова­тельностей-кодов можно получить, переставляя цифры в числе 010, т.е. векторов длины k = 3 из двухэлементного множества В = {0,1}, содержащих два нуля.

Имеется всего три разряда, которые обозначим р₁, р₂, р₃. Их можно переставить р₃ = 3! = 6 способами. Запишем различные получаемые сочетания разрядов и соответствующие коды:

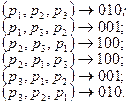
Видно, что коды повторяются тогда, когда несущественен порядок следования разрядов с одинаковой цифрой 0 (р₁, р₃). Все это соответствует тому факту, что имеются два способа (2!) пере­становки этих разрядов (р₁, р₃), (р₃, р₁) без изменения кода, т.е. неповторяющихся кодов будет меньше во столько раз, сколько имеется способов перестановки повторяющихся разрядов.

Рассмотрим более сложный случай. Определим, сколько различных «слов», не обязательно имеющих смысл, можно получить, переставляя буквы в слове «кишмиш»?

Здесь шесть букв слова можно переставить друг с другом р₆ = 6! = 720 способами, но в данном слове буквы «и» и «ш» повторяются дважды, и при их перестановке слова могут повто­ряться. Сколько же существует вариантов перестановок этих букв без изменения слова?

Первый вариант – исходный, второй – по­менять местами буквы «и», третий – поменять местами буквы «ш», четвертый – поменять местами как буквы «и», так и буквы «ш». Всего четыре варианта. С учетом того, что эти четыре вари­анта участвуют в порождении 720 способов, получим 720/4 = 180 различных «слов». Можно показать, что число раз, во сколько уменьшается количество слов по сравнению с числом перестано­вок без повторений, представляет собой произведение факториа­лов количества повторяющихся букв.

Таким образом, если из n элементов множества X = {х,, х₂, …, х_п} составлен вектор V длины k, причем каждому i-му компонен­ту можно поставить в соответствие число k_i, указывающее его число повторений в V, то задан вектор , который называется составом данного вектора.

Так, для множества X = {0, 1, 2, 3} и множества V = () задан вектор:

S = (2,1, 2,1).

Векторы одного и того же состава, отличающиеся лишь по­рядком компонентов, называются перестановками с повторени­ями данного состава.

Общая формула числа перестановок с повторениями данного состава имеет вид:

.

Пример 4

Сколько различных кодовых последовательностей можно получить перестановками кода 102202030?

Такому вектору, составленному из элементов множеств {0, 1, 2, 3}, соответствует вектор состава (1, 4, 3, 1), поэтому число раз­личных кодовых комбинаций определяется как число перестано­вок с повторениями этого состава:

.