Рассмотрим одно из центральных понятий математического анализа – понятие предела функции. Ввиду сложности для понимания этого понятия сначала дадим его описательное определение, подкрепленное примерами, а затем строгое определение.

Предел функции при x ® +¥

Пусть функция y = f(x) определена на множестве всех действительных чисел R или на бесконечном интервале (a, +¥).

Число b называют пределом функции  f(x) при стремлении x к +¥ (x® +¥), если значения f(x) приближаются к числу b как угодно близко при достаточно больших x.

Обозначение: .

Пример 1. Функция y =  определена на интервале  (0, +¥). Составим таблицу ее некоторых значений и построим ее график (рис. 1.2):

Из таблицы видно, что значения функции приближаются к числу 2 с увеличением x.

Убедимся, что  = 2.

Разность  показывает, на сколько отличается  f(x) от  2. Так, если x равно 10, то  f(x)  отличается от 2 на 1/10, а если x = 100, то  f(x) – 2 = 1/100. Разность f(x) – 2 может стать меньше любого заданного положительного числа e, если x взять достаточно большим. Например, e = 1/1000. Чтобы определить, для каких значений x выполняется неравенство  f(x) – 2 < 1/1000, надо решить это неравенство: , отсюда x > 1000.

Пусть e – произвольное (малое) положительное число, тогда найдется такое x₀, что f(x) – 2 < e для всех x  > x₀. Действительно, f(x) – 2 = , < e, x >. Обозначив x₀ = , получаем, что для всех  x, если x > x₀, то f(x) – 2 < e. Итак мы показали, что  = 2.

Пример 2. Функция y =  определена на  (–2, +¥). Выпишем таблицу ее некоторых значений и построим график (рис. 1.3).

Из таблицы значений и графика (рис. 1.3) видим, что с ростом x значения f(x) приближаются к 1, оставаясь меньше 1.

Покажем, что  =1. Разность f(x) – 1 отрицательна, поэтому вычислим ее абсолютную величину:

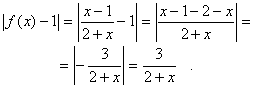
Покажем, что |f(x) – 1| может стать меньше любого заданного положительного числа e при достаточно больших x. Для этого решим неравенство  < e, получим:   2 + x  > ,  и  x  >  – 2.  Обозначим:  x₀  = 2. Таким образом, если x > x₀, то | f(x) – 1|  < . Например, возьмем в качестве e  число 0,01, тогда:

x₀ =  – 2 = 300 – 2 = 298,     x₀ = 298.

Если x > 298, то   < 0,01. Этим мы показали, что  = 1 (рис. 1.3).

Дадим строгое определение предела функции при x® +¥.

Число b называется пределом функции f(x) при стремлении x к  +¥, если для любого положительного числа e найдется такое число x₀, что для всех x, больших x₀, выполняется неравенство:

f(x) – b | < e .

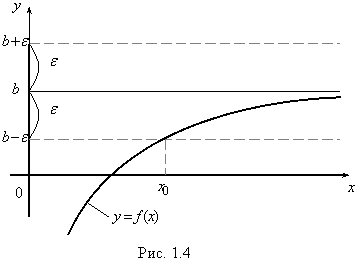
Геометрическая интерпретация этого определения приведена на рис. 1.4. В логических символах это определение выглядит так:

f(x) = b означает "e > 0 $x₀  "x > x₀  ( | f(x) – b | < e ).

Пример 3. Доказать, что  = 0   x Î (0, +¥).

Доказательство: f(x) = . Зафиксируем произвольное e > 0, покажем, что найдется такое x₀, что для всех x, больших x₀: | f(x) – 0 | < e. Действительно,

| f(x) – 0 | =   = ; < e   Û   x > .

Обозначим: x₀ = , тогда при x > x₀: |f(x) – 0 | < e, значит,    = 0.

Пусть для некоторой функции  y = f(x) f(x )= b, геометрически это означает, что точки графика y = f(x) приближаются к точкам прямой y = b (с той же абсциссой) при неограниченном возрастании x. В этом случае говорят, что прямая y = b является асимптотой графика y = f(x) при x® +¥. Неравенство: | f(x) – b | < e  равносильно двойному неравенству: b – e < f(x) < b + e. Из определения

предела следует, что по произвольному e > 0 найдется такое x₀, что для всех x, больших x₀, график  y = f(x) заключен внутри полосы, ограниченной прямыми: y = b + e,  y = b – e.