Определение. Пусть функция z = f(x, y) определена в некоторой области D. М₀(х₀, у₀) – внутренняя точка этой области. Функция z = f(x, y) в точке М₀(х₀, у₀) имеет максимум (минимум), если  (f(x₀, y₀) < f(х, у)) для всех точек (х, у) в некоторой окрестности точки М₀(х₀, у₀).Максимум или минимум функции называется ее экстремумом, а точка М₀(х₀, у₀) – точкой экстремума..

Если дифференцируемая функция  z = f(x, y)  достигает экстремума в точке   М₀(х₀, у₀), то ее частные производные первого порядка равны нулю в этой точке

Эти условия являются необходимыми условиями, а точки, в которых частные производные равны нулю, называются стационарными точками или "подозрительными" на экстремум. Не всякая стационарная точка является точкой экстремума. Поэтому возникает вопрос об условиях, достаточных для существования (или отсутствия) экстремума в стационарной точке.

Предположим, что М₀(х₀, у₀) – стационарная точка функции z = f(x, y).

Обозначим: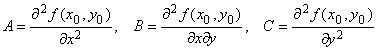  

и составим дискриминант  D = АС – В².  Тогда:

1) если D > 0, то функция имеет в точке М₀ экстремум, а именно: максимум при А < 0 (или С < 0) и минимум при А > 0 (или С > 0);

2) если D < 0, то в точке М₀ экстремума нет;

3) если D = 0, то требуется дальнейшее исследование ("сомнительный" случай).

Пример 1.21.  Найти экстремумы функции  z = x² + ху + у² – 3х – 6у.

Решение. 1) Находим частные производные первого порядка

записываем необходимые условия экстремума:

  .

Решая эту систему, находим стационарную точку: х = 0, у = 3, М₀(0, 3).

2) Находим частные производные второго порядка и величину D:

,  D = АС – В² = 2·2 – 1 = 3 > 0;   А > 0.

Следовательно, в точке М₀(0, 3) данная функция имеет минимум. Значение функции в точке минимума z_min = –9.