Рассмотрим функцию y = , аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция  не определена.

Теорема.  = 1 (первый замечательный предел).

Доказательство

1) Пусть a – положительный острый угол, докажем = 1. Предварительно докажем, что sina = 0 и cosa = 1.

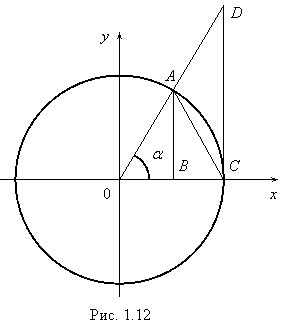
Рассмотрим окружность радиуса R       (рис. 1.12), OA = OC = R, тогда длина дуги АС равна: R×a,   АВ = R×sina.   Так как |AB| < ||, то 0 < sina < a.   Если a ® 0, то по теореме 8   (разд. 1.8) sina = 0. Докажем, что      cosa = 1. Так как cosa = 1 – 2sin², то на основании теорем о пределах получим:

cosa = (1 – 2sin²) = 1 – 2×0 = 1.

Вычислим теперь .

Из рис. 1.12 видим, что

S_DOAC < S_{секторOAC} < S_DODC.                                                    (*)

S_DOAC = R²sina,  S_{секторOAC} = R²×a,   S_DODC = R²tga.

Подставляя последние выражения в неравенства (*), находим:

R²sina < R²×a < R²tga.                                              (**)

Деля все части неравенства (**) на положительное число R²sina, получим:

1 <  <   или  1 >  > cosa                                                (***)

Применяя к неравенству (***) теорему о сжатой переменной при a  ®  0 получим:

 = 1 (ведь cosa = 1).

2) Пусть  x < 0,  x = –a,  тогда  a > 0,  ===1.

Итак, доказано, что  = 1, , а потому .

С помощью этого предела находятся многие другие пределы, содержащие тригонометрические функции.