Задача минимизации сети состоит в нахождении совокупности ребер, соединяющих все узлы сети (т.е. каждая пара узлов сети соединена цепью) и имеющих суммарную минимальную длину.

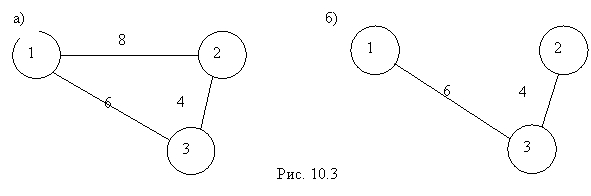Например, рассмотрим простую сеть (рис. 10.3). Ясно, что в минимальной сети узел (3) должен быть соединен с узлами (1) и (2), что дает суммарную длину последовательности ребер  (рис. 10.3, а).

Если соединить узлы 1 и 2, то появится цикл, что означает – сеть не является минимальной.

Очевидно, что решение задачи не должно содержать циклов, поэтому привело к названию минимальной сети – минимальное дерево-остов.

В любой сети минимальное дерево-остов можно определить следующим итеративным процессом:

Шаг 1. Выбрать произвольный узел.

Шаг 2. Выбранный узел соединить с ближайшим узлом сети. Соединенные узлы образуют теперь связанное множество, а остальные узлы – несвязанное множество.

Шаг 3. В несвязном множестве выбрать узел, который расположен ближе других (на кратчайшем расстоянии) к узлам связанного множества, т.е. узел для которого достигается , где i номера вершин связанного множества, а j номера вершин несвязанного множества, непосредственно соединенных дугами с вершинами связанного множества.

Шаг 4. Изменить соответствующим образом связанное и несвязанное множества и перейти к шагу 3.

Процесс повторять до тех пор, пока в связанное множество не попадут все узлы сети. В случае одинаково удаленных узлов выбрать любой из них, что будет означать неоднозначность минимального дерева-остова.

Пример 10.1

Построить набор дуг, соединяющих все вершины сети и имеющих минимальную протяженность.

Решение

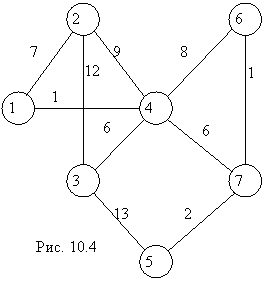
Итерация 1. Произвольно выбираем вершину сети (рис. 10.4). Пусть это будет вершина 1. Обозначим через С – множество связанных вершин;  – множество несвязанных вершин. Тогда

С = {1},  = {2, 3, 4, 5, 6, 7}.

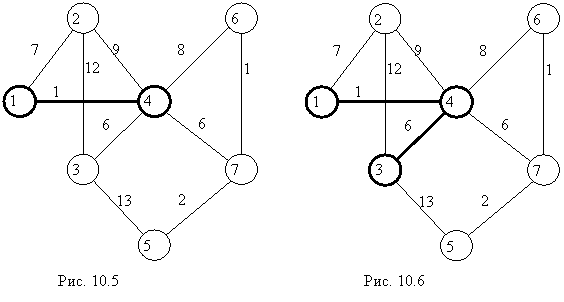Итерация 2. Ближе всех к связанному множеству вершин расположена вершина 4 (рис. 10.5), так как

.

Тогда изменяем множества связанных и несвязанных вершин:

C = {1, 4},  = {2, 3, 5, 6, 7}.

Итерация 3. Ближе всех к связанному множеству вершин расположены вершины 3 и 7 (рис 10.6), так как

.

Тогда изменяем множества связанных и несвязанных вершин, включая в множество связанных вершин, например, вершину 3:

C = {1, 4, 3},  = {2, 5, 6, 7}.

Итерация 4. Ближе всех к связанному множеству вершин расположена вершина 7 (рис. 10.7), так как

.

Тогда изменяем множества связанных и несвязанных вершин:

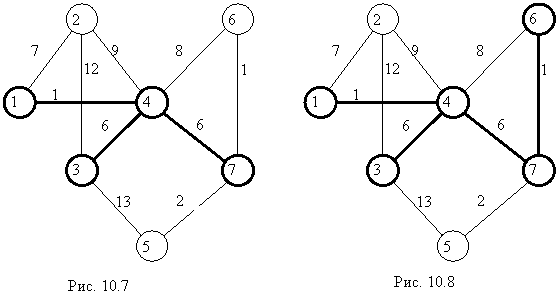C = {1, 4, 3, 7},  = {2, 5, 6}.

Итерация 5. Ближе всех к связанному множеству вершин расположена вершина 6 (рис. 10.8), так как

.

Тогда изменяем множества связанных и несвязанных вершин:

C = {1, 4, 3, 7, 6},  = {2, 5}.

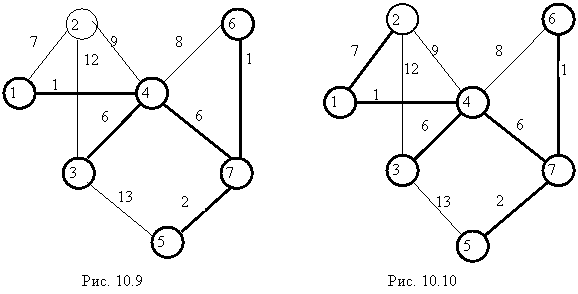
Итерация 6. Ближе всех к связанному множеству вершин расположена вершина 5 (рис. 10.9), так как

.

Тогда изменяем множества связанных и несвязанных вершин:

C = {1, 4, 3, 7, 6, 5},  = {2}.

Итерация 7. Ближе всех к связанному множеству вершин расположена вершина 2 (рис. 10.10), так как

.

Тогда изменяем множества связанных и несвязанных вершин:

С = {1, 4, 3, 7, 6, 5, 2}, .

В связанное множество попали все вершины, следовательно, минимальная сеть построена и ее суммарная длина равна:

.