Определение. Рассмотрим интегралы вида

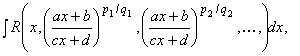
где R – рациональная функция;  – целые числа; а, b, с, d – некоторые постоянные.

Функция такого вида называется дробно-линейной иррациональностью.

Интегралы такого вида находятся с помощью подстановки ,

где n – наименьшее общее кратное чисел . В этом случае x и dx выражаются рационально через степени переменной t.

Пример 2.19. Найти

Решение. Подстановка  приводит интеграл к виду

При вычислении интегралов, содержащих радикалы вида

используются тригонометрические подстановки

соответственно.

Пример 2.20. Вычислить интеграл .

Решение. Подстановка  приводит интеграл к виду

.

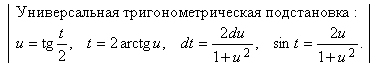
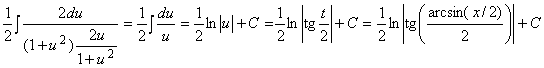Замечание. Имеются элементарные функции, интегралы от которых не выражаются через элементарные функции. Приведем несколько интегралов, "не берущихся в конечном виде":

Эти и подобные интегралы определяют новые виды функций, отличных от элементарных. Многие из этих функций имеют специальные названия: функция, определяемая первым интегралом, называется интегральным синусом, вторым – интегральным косинусом, третьим – интегральным логарифмом, четвертым и пятым – интегралами Френеля, последним – эллиптической функцией.

Заметим, что функции, определяемые с помощью интегралов, имеют обширные и важные применения в технике, естествознании и экономике. Для таких функций составлены таблицы их приближенных значений.

Например, найти в таблице интегралов Двайта интеграл вида

.

По оглавлению находим интегралы от рациональных алгебраических функций, затем находим страницу, где написано "Интегралы, содержащие ".  под № 160.21 и есть наш интеграл, но он  выражен через, который дан под  № 160.01, в конце концов, имеем (пусть  )

.
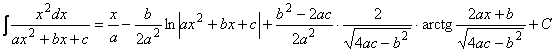