В главе 1 мы познакомились с приемами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, т.е. раскрытия неопределенностей типа  и . В этом разделе мы рассмотрим новый способ вычисления таких пределов, так называемое правило Лопиталя.

Теорема Лопиталя. (Раскрытие неопределенностей типа )

Пусть функции f(x), g(x) определены, непрерывны и дифференцируемы в точке x₀ и некоторой ее окрестности, причем g’(x) ¹ 0 для любого x из этой окрестности, и пусть

f(x₀) = 0, g(x₀) = 0 (следовательно, f(x), g(x) – бесконечно малые при). Если  существует, то существует и

=.                                           (2.18)

Доказательство. Равенство (2.18) называют правилом Лопиталя для раскрытия неопределенностей типа .

Дадим значению аргумента x₀ приращение Dx, такое, чтобы точка x = x₀ + Dx принадлежала рассматриваемой окрестности точки x₀.

Случай 1. Dx > 0, тогда x > x₀. Функции f(x), g(x), рассматриваемые на отрезке [x₀, x], удовлетворяют теореме Коши, поэтому найдется  такое   c Î (x₀, x), что выполняется равенство: =. Так как f(x₀) = g(x₀) = 0, то получим: =. Заметим, что число c зависит от x, но если , то , так как x₀ < c < x. Переходя к пределу в последнем равенстве, получаем:

===.

Случай 2. Dx < 0, тогда x < x₀. Функции f(x), g(x), рассматриваемые на отрезке [x, x₀], удовлетворяют условиям теоремы Коши, и потому доказательство аналогично, как в случае 1. Итак, теорема Лопиталя доказана.

Пример 1. Найти .

Решение. Поскольку функции f(x) =1 – cos3x, g(x) = 2x удовлетворяют условию теоремы Лопиталя, то  = = = 0.

Замечание 1. Теорема Лопиталя справедлива и в том случае, когда функции f(x), g(x) не определены в точке x₀, но f(x) = 0 и g(x) = 0. В самом деле, если доопределить f (x), g(x), положив f(x₀) = g(x₀) = 0, тогда f(x), g(x) будут непрерывны в точке x₀, а потому теорема Лопиталя будет применима к ним.

Замечание 2. Правило Лопиталя применимо и в том случае, когда

f(x) = 0, g(x) = 0.

Действительно, введя новую переменную  y =, видим, что y ® 0 при x ® ¥. Тогда                  =  =  = .

Теорема Лопиталя. (Раскрытие неопределенностей типа )

Пусть функции f(x), g(x) дифференцируемы в окрестности точке x₀, за исключением самой точки x₀, причем g’(x) ¹ 0, и пусть f(x) = ¥, g(x) = ¥. Если существует , то существует   и =.

Доказательство этой теоремы мы не приводим, его можно найти в учебниках.

Отметим, что эта теорема верна для случая, когда x®¥, в этом можно убедиться, повторяя рассуждения замечания 2.

Замечание 3. Предел отношения двух функций может существовать, в то время как предел отношения их производных не существует.

Например, = 1, а = (1 + cosx) – не существует, так как cosx не существует.

Замечание 4. Если  при x ® x₀ (x ® ¥) является неопределенностью типа  или , и (x), g’(x) удовлетворяют условиям теоремы Лопиталя, то

==.

Таким образом, для раскрытия неопределенностей типа  или  иногда приходится применять правило Лопиталя несколько раз.

Пример 2. Найти .

Решение. При x ® 0 и x > 0 lnx = ¥, ctgx = ¥, следовательно, имеем отношение двух бесконечно больших при x ® 0 и неопределенность типа . Вычислим:

 =  = –= –= 0.

Замечание 5. Теорема Лопиталя остается верной и тогда, когда = ¥.

Пример 3. Найти .

Решение. Имеем неопределенность типа . Применяя теорему Лопиталя два раза, получим:  =  =  = ¥.

Можно показать, что для любого nÎN   = ¥. Это означает, что показательная функция e^x растет быстрее любой степенной функции xⁿ.

Рассмотрим неопределенности других видов.

Если a(x) = 0, F(x) = ¥, то a(x)×F(x) называют неопределенностью типа 0×¥, а [F(x)]^a(x) – неопределенностью типа ¥⁰.

Если F₁(x) = +¥, F₂(x) = +¥, то (F₁(x) – F₂(x)) – неопределенность типа ¥ – ¥.

Аналогично понимаются и другие неопределенности. При раскрытии таких неопределенностей зачастую помогает способ сведения их к неопределенностям типа  или  с последующим применением правила Лопиталя.

Пример 4. Найти x²lnx.

Решение. Так как lnx = ¥, то имеем неопределенность типа 0×¥. Преобразуем ее к виду :  x²lnx = , затем применим правило Лопиталя,

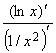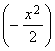 =  =  =  = 0.  Итак, x²lnx = 0.