Теорема 1. (Достаточное условие возрастания функции)

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), причем (x) > 0 для любого xÎ(a, b), то эта функция возрастает на отрезке [a, b].

Доказательство. Функция возрастает на [a, b], если

"x₁, x₂Î[a,b] (x₁ < x₂ ®  f(x₁) < f (x₂)).

Пусть x₁, x₂ – любые два числа из [a, b], такие, что x₁ < x₂. Докажем, что  f(x₁) < f(x₂).

По теореме Лагранжа о конечных приращениях f (x₂) – f (x₁) = (с)(x₂ – x₁), где c удовлетворяет неравенству x₁ < c < x₂. По условию теоремы (с) > 0, следовательно, f(x₂) – f (x₁) > 0, т.е.  f (x₁) < f (x₂). Теорема доказана.

Теорема 2. (Необходимое условие возрастания функции)

Если функция f(x) непрерывна и возрастает на отрезке [a, b], дифференцируема на интервале (a, b), то (x) ³ 0 для любого x из интервала (a, b).

Доказательство. Пусть x₀Î(a, b). Дадим аргументу приращение Dx, тогда функция получит приращение f(x₀ + Dx) – f(x₀). Функция f(x) возрастает на [a, b], поэтому, если Dx > 0,  то f(x₀ + Dx) – f(x₀) > 0, а если Dx < 0, то  f(x₀ + Dx) – f(x₀) < 0. В обоих случаях > 0, а потому ³ 0, т.е. (x₀) ³ 0. Теорема доказана.

Аналогичные теоремы справедливы для убывающей функции, только условие (x) > 0 заменяется на условие: (x) < 0.

Сформулируйте и докажите достаточное условие и необходимое условие для убывания функции.

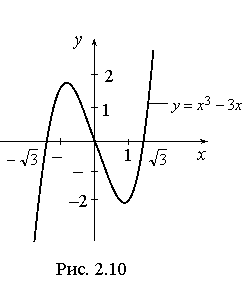Пример. Исследовать на монотонность (т.е. возрастание и убывание) функцию:

f (x) = x³  – 3x.

Решение. (x) = 3x² – 3 = 3(x² – 1).

Неравенство (x) > 0, т.е. 3(x² – 1) > 0, справедливо для x < –1 и для x >1. Следовательно, функция f(x) возрастает на интервалах (–¥, –1) и        (1, +¥). Поскольку неравенство (x) < 0, т.е.         3(x² – 1) < 0 справедливо для  xÎ(–1, 1), то на интервале (–1, 1) функция f(x) убывает.

Построим график функции y = x³ – 3x     (рис. 2.10), используя ее значения в точках:

x₁ = –1,    x₂ = 1,   x₃ = 0,   x₄ = –,    x₅ =:

 f(–1) = 2,    f(1) = –2,   f(0) = 0,  f(–) = 0,  f() = 0.

Заметим, что в точке x₁ = –1 значение f(–1) больше, чем значение f(x) в соседних с x₁ точках. Говорят, что в точке x₁ функция имеет максимум (локальный максимум). Аналогично,  f(x₂) < f(x) для x, близких к x₂. В этом случае говорят, что в точках x₂ функция имеет минимум (локальный минимум).