Основная форма записи комплексного числа – алгебраическая форма записи:

z = х + iy.

Из алгебраической записи z = х + iy и  формулы (2.4) получаем:

).

Полученная форма записи называется тригонометрической формой комплексного числа:

.                                                            (2.9)

Модуль комплексного числа есть однозначная функция:

,                                                     (2.10)

Условие равенства ненулевых комплексных чисел эквивалентно тому, что их модули равны, а аргументы могут отличаться на слагаемое 2 (к = 0, ± 1, ±2,…).

Используем формулу Эйлера:

,                                                (2.11)

из формулы z = х + iy получим показательную форму записи комплексного числа:

                                                        (2.12)

Важно помнить, что между комплексными числами не вводится отношения неравенства, т.е. неравенство z₁ < z₂, во­обще говоря, не имеет смысла. Однако комплексные числа мож­но сравнивать по модулю.

Определение. Суммой  z₁ + z₂ двух комплексных чисел  z₁ = x₁ + iy₁ и  z₂ = x₂ + iy₂ называется комплексное число:

z = (x₁ +x₂) + i(y₁+ y₂).                                              (2.14)

Определение. Разностью z_{1 –} z₂ двух комплексных чисел называется комплексное число z, вида:

.               (2.15)

Определение. Произведением z₁, z₂ комплексных чисел z₁= x₁ +iy₁ и z₂= x₂ +iy₂ называется комплексное число:

                                   (2.16)

Отметим, что. Используя формулу (2.4), получим произведение комплексных чисел в тригонометрической и показательной формах записи:

;                            (2.17)

.                                                 (2.18)

Из формул (2.17) и (2.18) следует, что при умножении числа  на , вектор  растягивается (сжимается) в  раз и по­ворачивается на угол   против часовой стрелки. Умножение допускает обратную операцию, называемую делением.

Определение. Число z = х + iy называется частным чисел z₁ = x₁ +iy₁ и z₂ = x₂ +iy₂,   , если:

z₂z = z₁                                                       (2.19)

Преобразуем :

                    (2.20)

Используя в выражении (2.20) формулы (2.4), получим ча­стное в показательной и тригонометрической формах:

;                                                  (2.21)

.                                (2.22)

Из формул (2.21) и (2.22) видно, что при делении комплексных чисел модуль числителя делится на модуль знаменателя, и из аргумента числителя вычитается аргумент знаменателя:

;                 .                          (2.23)

Определение. Натуральная степень комплексного числа z определяет­ся равенством:

.                                                           (2.24)

Используя в выражении (2.24) формулы (2.4), получим три­гонометрическую и показательную формы записи возведения в степень комплексного числа:

;                                         (2.25)

.                                                          (2.26)

При r = 1 формула (2.25) имеет вид:

.                                           (2.27)

Формула (2.27) называется   формулой Моавра.

Определение. Комплексное числоW называется корнем степени n из числа z, , если .

Положив

и используя формулу (2.25), получим:

;                                                   (2.28)

,                                    (2.29)

где к = 0,1, 2,…,n -1.

Из формул (2.28) и (2.29) следует:

.                                                      (2.30)

Пример

Даны комплексные числа  и . Необходимо найти:  .

Решение

Производим действия над комплексными числами:

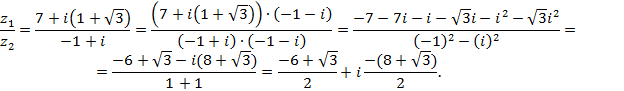
Используя формулу (2.25), получим:

.

Найдем модуль

Найдем , используя формулу (2.8):

;

Найдем  используя формулу (2.29):

· при k = 0

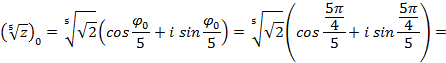
· при k = 1

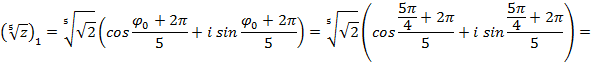
· при k = 2
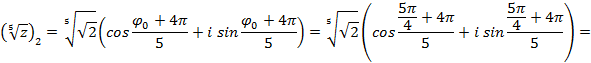