Пусть функция y = f (x) определена на некотором промежутке X, x₀ÎX и f(x) дифференцируема в точке x₀, т.е. производная  существует.

Для одной и той же функции  f(x) производную можно вычислять в различных точках x, и ее значения будут зависеть от x, т.е. производная (x) будет функцией от x, ее называют производной функцией от функции f(x). Нахождение производной функции называют дифференцированием функции f(x).

Итак, производная функция от функции  f(x) по определению:

Для того чтобы научиться дифференцировать функции, надо знать производные основных элементарных функций и правила дифференцирования. Выведем производные некоторых элементарных функций.

1. f(x) = с – постоянное число.

Итак,  (c)‘ = 0.

1. f(x) = x:

Получили:  (x)‘ = 1.

2. :

.

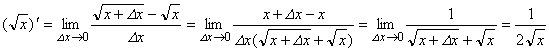Таким образом,  .

3. :

.

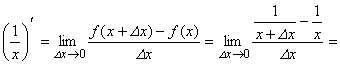
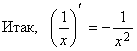4. f(x) = sinx:

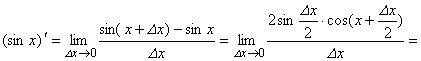
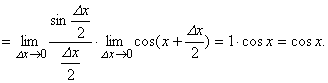
Значит,  (sinx)‘ = cosx

5. Аналогично доказывается, что (cosx)’ = –sinx.

Для дальнейшего изложения вычислим два вспомогательных предела, а именно:

,

используя для этого второй замечательный предел и непрерывность функций log_ax и a^x.

Первый предел:

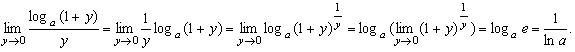
Таким образом, .

Для вычисления второго предела введем новую переменную: z = a^y – 1, тогда a^y = z + 1, откуда  y = log_a(z + 1). Если y ® 0, то z ® 0, следовательно,

,   т.е. .

7.   :

.

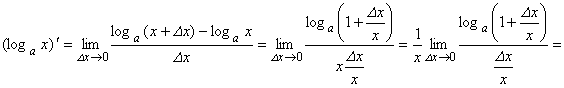
Значит,     В частности, .

8.   Убедимся, что (a^x)‘ = a^xlna:

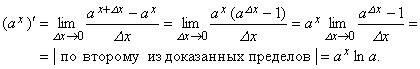
При a = e, получаем: (e^x)‘ = e^x.

Производные для других элементарных функций мы вычислим в следующих разделах.