Приведем таблицу основных интегралов. Каждая из нижеследующих формул верна на каждом промежутке, принадлежащем области определения подынтегральной функции. Часть формул этой таблицы непосредственно следует из определения интегрирования как операции, обратной к дифференцированию, и таблицы производных. Справедливость остальных формул легко проверить дифференцированием.

Таблица интегралов

1) .

2)

3)

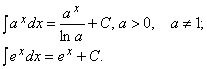
4)  

5)  

6)  

7)  

8)  

9)  

10)  

11)

12)

13)                   14)      

15)                          16)      

Например, проверим справедливость формулы 1  непосредственно дифференцированием (см. определение неопределенного интеграла), так как производная правой части

равна подынтегральной функции левой части, то формула верна. ■

Докажем  второе равенство. Пусть . Тогда  и  . Если   , то   и

, то есть в обоих случаях производная правой части равна подынтегральной функции левой части. ■

Аналогично доказываются остальные формулы.