Определение. Если функция  определена на кусочно-гладкой кривой L и точки   этой кривой раз­бивают ее на n элементарных дуг, в каждой из которых выбрана точка  то , называется интегралом от f(z) по кривой L и обозначается  или, в случае замкнутого контура L   .

Если функция   непрерывна на L, то интеграл существует (его часто называют контурным):

,       (2.34)

где

     и     

являются криволинейными интегралами от функций двух действительных переменных.

Если кривая L задана параметрическими уравнениями:

      

и каждая из этих функций гладкая, то

.          (2.35)

Известно, что вместо двух вещественных параметриче­ских уравнений линии L можно ввести одно эквивалентное им комплексно-параметрическое уравнение

,

тогда уравнение (2.35) можно переписать так:

 .                                     (2.36)

Формула (2.36) удобна для вычисления контурных интегра­лов.

Теорема 1 (основная теорема Коши). Если функция f(z) аналитична в односвязной области, то для любого кусочно-гладкого замкнутого контура L, лежащего в этой области,

.

Следствие. Если функция f(z) аналитична в односвязной замкнутой области, ограниченной кривой L, то

.

Заметим, что из теоремы Коши следует: если функция f(z) аналитична в односвязной области D, то для любой незамк­нутой кривой L, принадлежащей D, интеграл от f(x) по L за­висит только от начальной точки z₀ и конечной точки z, т.е. от формы кривой (пути) L не зависит. При этом:

,                                          (2.37)

где F(z) – одна из первообразных функций для f(z), т.е. F’(z) = f(z). Формула (2.37) называется формулой Ньютона-Лейбница.

Теорема 2. Если функция f(z) аналитична в замкнутой области  (односвязной или многосвязной) и L – граница D, то для любой точки z₀, лежащей внутри этой области, справедливы следую­щие формулы:

;                                            (2.38)

                              (2.39)

Интеграл в правой части формулы (2.39) называется интегралом Коши для функции f(z), а сама эта формула носит название инте­гральной формулы Коши.

Формулу (2.39) часто называют интегральной формулой Коши для n-й производной функции f(z), и она выражает тот факт, что аналитическая функция, заданная в замкнутой области , дифференцируема сколько угодно раз в каждой точке z области D (следовательно, производные f’(z), f’’(z),,… аналитичны в точке z).

Отметим, что формула (2.39) получается из интегральной формулы Коши (2.38) в результате последовательного дифференцирования n раз по z₀ под знаком интеграла.

Пример 1

Вычислить контурный интеграл  где L – прямолинейный отрезок, соединяю­щий точку z = 0 с точкой z = 3+7i.

Решение

1) Сделаем схематический рисунок пути (контура) ин­тегрирования (рис. 2.3).

2) Составим параметрические уравнения или комплекс­но-параметрическое уравнение пути (контура) интегрирования. Если путь интегрирования состоит из прямолиней­ных участков, то целесообразно использовать формулу для пря­мой, проходящей через две заданные точки:

Из условия z = 0, следует, что

;

из условия z = 3+7i, следует, что

.

Получаем:

,

отсюда

3) Установим, как изменяется параметр t при движении от точки z = 0 до точки z = 3 + 7i.

При  z = 0 у нас х = 0 и у = 0, а значит, из параметрических уравнений t = 0; при z = 3 + 7i имеем x = 3 и у = 7, тогда из тех же уравнений находим t = 1.

Таким образом, . Используем формулу (2.36):

Ответ:

Замечание. Если путь интегрирования состоит из двух отрезков, то составляются параметрические уравнения для каждого участка отдельно и находятся два интеграла.

Пример 2

Построить область, заданную на комплексной плоскости

.

Решение

Запишем область в другом виде с учетом, что  получим:

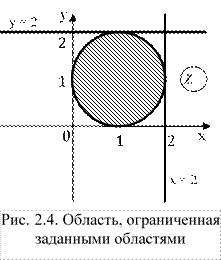
Это область, ограниченная окружностью с центром в точке (1, 1) и радиусом 1.

Ограничение  запишем в виде:

.

Ограничение  имеет вид:

.

Получили область, ограниченную графиками:

;

.

Изобразим область на графике (рис. 2.4). Заданная область заштрихована.

Пример 4

Найти интеграл от функции комплексного переменного, используя основную теорему Коши:

.

Решение

1) Построим область интегрирования:

получим

;

, .

Получили уравнение окружности с центром в точке О и радиусом  (рис. 2.5).

2) Найдем точки  и изобразим их на рисунке 2.5.

Из формулы (2.38) следует, что

.

Получаем, что  . Точка не попадает в область интегрирования, следовательно,

.

1) Определяем интеграл, используя формулу (2.38):

 

.

Получаем:

;

 .

Ответ:

Пример 5

Найти интеграл от функции комплексного переменного используя основную теорему Коши:  .

Решение

1) Построим область интегрирования:

.

Получим:

;

;

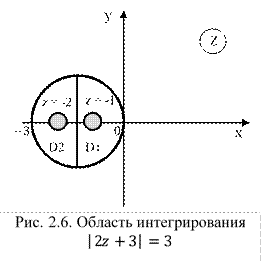
Получили уравнение окружности с центром в точке О и радиусом   (рис. 2.6).

2) Найдем точки  и изобразим их на рисунке 2.6.

Из формулы (2.38) следует, что

 .

Обе точки лежат в области интегрирования, следовательно,  разбиваем область интегрирования на две замкнутые области D1 и D2. Интеграл разбиваем на два:

.

3) Определяем интегралы, используя формулу (2.38), найдем интеграл по области D1, где :

 

  

.

Получаем:

;             .

Найдем интеграл по области D2, где :

 

  

 .

Получаем:

;               .

Складываем полученные интегралы и получаем:

Ответ: 2