Определение. Точки комплексной плоскости, в которых однозначная функция f(z) является аналитической, называют правильными точками этой функции, а точки, в которых f(z) не является аналитиче­ской, называют особыми точками (в частности, точки, в которых f(z) не определена).

Определение. Точка z₀ называется нулем (корнем) порядка (кратности) аналитической функции f(z),если:

а)

б)  существует, конечен и не равен нулю.

Если  целые положительные числа), то­гда  – нули (корни) этого многочлена, которые имеют соответственно порядки (кратности) .

Определение. Пусть f(z) аналитическая функция в окрестности точки z₀, за ис­ключением самой точки z₀. В этом случае точка z₀ называется изолированной особой точкой функции f(z).

Различают изолированные особые точки одно­значной функции трёх типов:

1) устранимую особую точку – изолированную особую точку z₀ , в которой существует конечный предел:

;                                                 (2.40)

2) полюс k-го порядка – изолированную особую точку z₀, в которой существует конечный предел, не равный нулю:

                                                    (2.41)

если , то z₀ – полюс первого порядка (простой полюс);

3) сущест­венно особую точку – изолированную особую точку z₀, которая не является ни уст­ранимой, ни полюсом. То есть   не существует, ни конечный, ни бесконечный.

Теорема (о связи между нулем и полюсом). Если точка z₀  – нуль порядка к функции f(z), то для функции 1/f(z) эта точка является полюсом порядка к.

Пусть f(z) – функция, аналитическая в каждой точке об­ласти D, за исключением конечного числа изолированных осо­бых точек, и L — кусочно-гладкий замкнутый контур, целиком лежащий в области D и не проходящий через особые точки функции f(z).

Если в области, ограниченной контуром L, не содержится особых точек функции   f(z), то по основной теореме Коши

.

Если же в области, ограниченной контуром L, имеются особые точки функции f(z), то значение этого интеграла, вообще говоря, отлично от нуля.

Определение. Вычетом аналитической функции f(z) относительно изо­лированной особой точки z₀ (или в точке z₀) называется комплексное число, равное значению интеграла  , где L – любой кусочно-гладкий замкнутый контур, лежащий в облас­ти аналитичности функции f(z) и содержащий внутри себя един­ственную особую точку z₀ функции f(z).

Вычет f(z) относительно точки z₀ обозначается симво­лом resf(z₀)(Resf(z₀)) или  так, что имеем:

.                                        (2.42)

Вычет функции относительно устранимой особой точки равен нулю:

.                                                   (2.43)

Вычет f(z) относительно простого полюса  можно найти по формуле:

.                                      (2.44)

Вычет f(z) относительно полюса порядка к находят по формуле:

.                                 (2.45)

Если причем точка  является простым нулем и не является нулем для , то:

.                                                 (2.46)

Основная теорема Коши о вычетах. Если функция f(z) аналитическая в замкнутой области , ограниченной контуром L, за исключением конечного числа особых точек , лежащих внутри ,то:

.                               (2.47)

Эта теорема имеет большое значение для приложений. Од­но из них – это вычисление некоторых интегралов от функции комплексной переменной.

Замечание. В предыдущих рассуждениях о вычетах неявно предпола­галось, что рассматриваются конечные изолированные особые точки (это ясно из того, что интеграл по замкнутому контуру по умолчанию брался в положительном направлении, т.е. против часовой стрелки, а особая точка при этом попадает внутрь конту­ра только в случае, когда она конечна). В случае же, когда рас­сматривается бесконечно удаленная точка, ситуация несколько иная. Точнее, сформулируем это так.

Определение. Вычетом функции f(z) относительно бесконечно уда­ленной точки  называют интеграл:

,

где L – замкнутый кусочно-гладкий контур, целиком лежащий в той ок­рестности точки , в которой функция f(z) является анали­тической. Интегрирование по Lсовершается в отрицательном направлении этого контура, т.е. так, чтобы при обходе контура бесконечно удаленная точка оставалась слева. Таким образом:

                                        (2.48)

Пример 1

Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:

.

Решение

1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):

Особые точки:   .

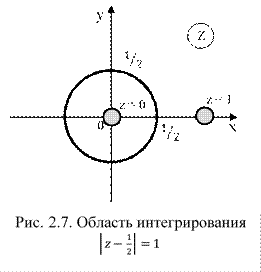
2) Определим точки, лежащие внутри области интегрирования, изобразим область  графически (рис. 2.7).

Точку z = 1 не рассматриваем, так как она не лежит внутри области .

3) Определим тип рассматриваемой изолированной особой точки z = 0. Найдем предел по формуле (2.41):

Так как предел существует, то z = 0 – полюс первого порядка (простой полюс).

4) Найдем вычет функции  относительно простого полюса z = 0, используя формулу (2.44):

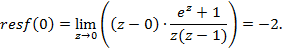
5) Определим значение интеграла по основной теореме Коши о вычетах (2.47):

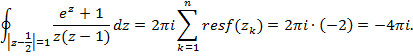
Ответ

Пример 2

Найти интеграл от функции комплексного переменного,  используя основную теорему Коши о вычетах:

.

Решение

1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):

Особые точки:   .

2) Определим точки, лежащие внутри области интегрирования, изобразим область  (рис. 2.8).

Обе особые точки   лежат внутри области интегрирования.

3) Определим тип рассматриваемых изолированных особых точек  . Найдем предел по формуле (2.41):

а)

так как предел существует, то z = -1 – полюс первого порядка (простой полюс).

б)

так как предел существует, то z = -2 – полюс первого порядка (простой полюс).

4) Найдем вычеты функции  относительно простых полюсов и      используя формулу (2.44):

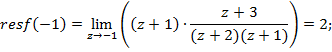
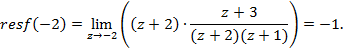
5) Определим значение интеграла по основной теореме Коши о вычетах (2.47)

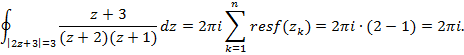
Ответ: 2