Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):

  .                                                               (2.2)

Для каждого значения t из некоторого интервала соответствуют определенные значения x и y, а, следовательно, определенная точка M (x, y) плоскости. Когда t пробегает все значения из заданного интервала, то точка M (x, y) описывает некоторую линию L. Уравнения (2.2) называются параметрическими уравнениями линии L.

Если функция x = j(t) имеет обратную t = F(x), то подставляя это выражение в уравнение y = g(t), получим y = g(F(x)), которое задает y как функцию от x. В этом случае говорят, что уравнения (2.2) задают функцию y параметрически.

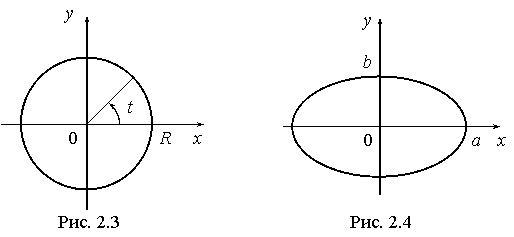
Пример 1. Пусть M (x, y) – произвольная точка окружности радиуса R и с центром в начале координат. Пусть t – угол между осью Ox и радиусом OM (см. рис. 2.3). Тогда x, y выражаются через t:

  ,   0 £ t £ 2p,                                          (2.3)

Уравнения (2.3) являются параметрическими уравнениями окружности. Исключим из уравнений (2.3) параметр t. Для этого каждое из уравнений возведем в квадрат и сложим, получим:   x² + y² = R²(cos²t + sin²t)   или   x² + y²  = R² – уравнение окружности в декартовой системе координат. Оно определяет две функции: y = и y = –.

Каждая из этих функций задается параметрическими уравнениями (2.3), но для первой функции  t Î [0, p], а для второй  t Î [p, 2p].

Пример 2. Параметрические уравнения

  ,   0 £ t £ 2p                                          (2.4)

задают эллипс с полуосями a, b (рис. 2.4). Исключая из уравнений параметр t, получим каноническое уравнение эллипса:

 + = 1.

Пример 3. Циклоидой называется линия, описанная точкой, лежащей на окружности, если эта окружность катится без скольжения по прямой (рис. 2.5). Введем параметрические уравнения циклоиды. Пусть радиус катящейся окружности равен a, точка M, описывающая циклоиду, в начале движения совпадала с началом координат. Определим координаты x, y точки M после того, как окружность повернулась на угол t

(рис. 2.5), t = ÐMCB. Длина дуги MB равна длине отрезка OB, так как окружность катится без скольжения, поэтому

OB = at,    AB = MD = asint,    CD = acost,     x = OB – AB = at – asint = a(t – sint),

y = AM = CB – CD = a – acost = a(1 – cost).

Итак, получены параметрические уравнения циклоиды:

                                                       (2.5)

При изменении параметра t от 0 до 2p окружность поворачивается на один оборот, при этом точка M описывает одну арку циклоиды. Уравнения (2.5) задают y как функцию от x. Хотя функция x = a(t – sint) имеет обратную функцию, но она не выражается через элементарные функции, поэтому функция y = f(x) не выражается через элементарные функции.

Рассмотрим дифференцирование функции, заданной параметрически уравнениями (2.2). Функция x = j(t) на некотором интервале изменения t имеет обратную функцию t = F(x), тогда y = g(F(x)). Пусть  x = j(t), y = g(t) имеют производные, причем  ¹ 0. По правилу дифференцирования сложной функции . На основании правила дифференцирования обратной функции ,  поэтому:

.                                                                   (2.6)

Полученная формула (2.6) позволяет находить производную для функции, заданной параметрически.

Пример 4. Пусть функция y, зависящая от x, задана параметрически:

   0 £ t £ p.    Найти .

Решение.     =  = –ctgt.

Пример 5. Найти угловой коэффициент k касательной к циклоиде в точке M₀, соответствующей значению параметра t₀ = .

Решение. Из уравнений циклоиды:  = asint,   = a(1 – cost), поэтому

 =  = .

Угловой коэффициент касательной в точке M₀ равен значению  при t₀ = :

k = 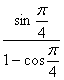==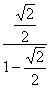===+1,   k = +1.