Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т. е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной. Он основан на следующей теореме.
Теорема 2.2 Пусть функция ![]() определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция
определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция ![]() . Тогда, если на множестве Х функция
. Тогда, если на множестве Х функция ![]() имеет первообразную, то на множестве Т справедлива формула
имеет первообразную, то на множестве Т справедлива формула
![]()
Доказательство: Найдем производные по переменной ![]() от обеих частей равенства:
от обеих частей равенства:
![]() ,
,
![]()
(смотри свойство 1 неопределенного интеграла).
Так как ![]() , то эти производные равны, поэтому по следствию из теоремы Лагранжа левая и правая части отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до константы, то указанную постоянную в окончательной записи можно опустить.■
, то эти производные равны, поэтому по следствию из теоремы Лагранжа левая и правая части отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до константы, то указанную постоянную в окончательной записи можно опустить.■
Функцию ![]() стараются выбирать таким образом, чтобы правая часть этой формулы приобрела более удобный для интегрирования вид. Когда же интеграл относительно новой переменной t вычислен, с помощью обратной подстановки
стараются выбирать таким образом, чтобы правая часть этой формулы приобрела более удобный для интегрирования вид. Когда же интеграл относительно новой переменной t вычислен, с помощью обратной подстановки ![]() возвращаются к переменной x.
возвращаются к переменной x.
Пример 2.8. Вычислить интеграл ![]() , сделав замену переменной.
, сделав замену переменной.
Решение. Положим ![]() тогда
тогда ![]() таким образом
таким образом
![]()
Пример 2.9. Вычислить ![]()
Решение.
![]()
![]()
Примеры 2.5, 2.6, 2.7 можно решить, сделав замену переменной. Однако не всегда сразу видно какую замену надо сделать.
Пример 2.![]() . Найти интеграл
. Найти интеграл ![]()
Решение. ![]()
![]()
Пример 2.![]() . Найти интеграл
. Найти интеграл ![]()
Решение. 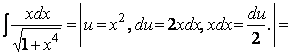
![]()
Пример 2.![]() . Найти интеграл
. Найти интеграл ![]()
Решение. 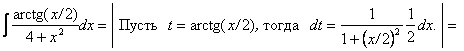
![]()