Пусть функция в точке x0 имеет производную. По определению: ![]() =
= ![]() (x0), поэтому по свойствам предела (разд. 1.8)
(x0), поэтому по свойствам предела (разд. 1.8) ![]() = f(x0) + a, где a – бесконечно малая при Dx ® 0. Отсюда
= f(x0) + a, где a – бесконечно малая при Dx ® 0. Отсюда
Dy = ![]() (x0)Dx + a×Dx. (2.7)
(x0)Dx + a×Dx. (2.7)
При Dx ® 0 второе слагаемое в равенстве (2.7) является бесконечно малой высшего порядка, по сравнению с Dx: ![]()
![]() =
= ![]() a = 0, поэтому Dy и
a = 0, поэтому Dy и ![]() (x0)×Dx – эквивалентные, бесконечно малые (при
(x0)×Dx – эквивалентные, бесконечно малые (при ![]() (x0) ¹ 0).
(x0) ¹ 0).
Таким образом, приращение функции Dy состоит из двух слагаемых, из которых первое ![]() (x0)×Dx является главной частью приращения Dy, линейной относительно Dx (при
(x0)×Dx является главной частью приращения Dy, линейной относительно Dx (при ![]() (x0) ¹ 0).
(x0) ¹ 0).
Дифференциалом функции f(x) в точке x0 называется главная часть приращения функции и обозначается: dy или df (x0). Следовательно,
df (x0) = ![]() (x0)×Dx. (2.8)
(x0)×Dx. (2.8)
Пример 1. Найти дифференциал функции dy и приращение функции Dy для функции y = x2 при:
1) произвольных x и Dx; 2) x0 = 20, Dx = 0,1.
Решение
1) Dy = (x + Dx)2 – x2 = x2 + 2xDx + (Dx)2 – x2 = 2xDx + (Dx)2, dy = 2xDx.
2) Если x0 = 20, Dx = 0,1, то Dy = 40×0,1 + (0,1)2 = 4,01; dy = 40×0,1= 4.
Запишем равенство (2.7) в виде:
Dy = dy + a×Dx. (2.9)
Приращение Dy отличается от дифференциала dy на бесконечно малую высшего порядка, по сравнению с Dx, поэтому в приближенных вычислениях пользуются приближенным равенством Dy » dy, если Dx достаточно мало.
Учитывая, что Dy = f(x0 + Dx) – f(x0), получаем приближенную формулу:
f(x0 + Dx) » f(x0) + dy. (2.10)
Пример 2. Вычислить приближенно ![]() .
.
Решение. Рассмотрим: f(x) = ![]() ; x0 = 4, Dx = 0,1; тогда
; x0 = 4, Dx = 0,1; тогда ![]() = f(x0 + Dx). Используя формулу (2.10), получим:
= f(x0 + Dx). Используя формулу (2.10), получим:
![]() = f(x0 + Dx) » f(x0) + dy, f(x0) =
= f(x0 + Dx) » f(x0) + dy, f(x0) = ![]() =2, dy = f’(x0)×Dx =
=2, dy = f’(x0)×Dx = ![]() ×0,1 =
×0,1 = ![]() = 0,025.
= 0,025.
Значит, ![]() » 2,025.
» 2,025.
Рассмотрим геометрический смысл дифференциала df(x0) (рис. 2.6).
Проведем к графику функции y = f(x) касательную в точке M0(x0, f(x0)), пусть j – угол между касательной KM0 и осью Ox, тогда f’(x0) = tgj. Из DM0NP: PN = tgj×Dx = f’(x0)×Dx = df(x0). Но PN является приращением ординаты касательной при изменении x от x0 до x0 + Dx.
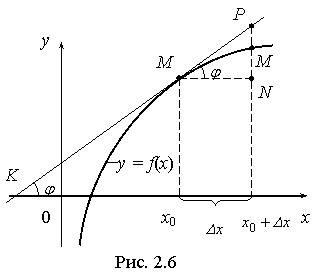 Следовательно, дифференциал функции f(x) в точке x0 равен приращению ординаты касательной.
Следовательно, дифференциал функции f(x) в точке x0 равен приращению ординаты касательной.
Найдем дифференциал функции y = x. Так как (x)‘ = 1, то dx = 1×Dx = Dx. Будем считать, что дифференциал независимой переменной x равен ее приращению, т.е. dx = Dx.
Если x – произвольное число, то из равенства (2.8) получаем df(x) = ![]() (x)dx, откуда
(x)dx, откуда ![]() (x) =
(x) = ![]() или
или ![]() (x) =
(x) = ![]() .
.
Таким образом, производная для функции y = f(x) равна отношению ее дифференциала к дифференциалу аргумента.
Рассмотрим свойства дифференциала функции.
Если u(x), v(x) – дифференцируемые функции, то справедливы следующие формулы:
d(u + v) = du + dv; (2.11)
d(u×v) = u×dv + v×du; (2.12)
d![]() =
= ![]() , (v ¹ 0). (2.13)
, (v ¹ 0). (2.13)
Для доказательства этих формул используются формулы производных для суммы, произведения и частного функции. Докажем, например, формулу (2.12):
d(u×v) = (u×v)‘Dx = (u×v’ + u’×v)Dx = u×v’Dx + u’Dx×v = u×dv + v×du.
Рассмотрим дифференциал сложной функции: y = f(x), x = j(t), т.е. y = f(j(t)).
Тогда dy = ![]() dt, но
dt, но ![]() =
= ![]() , поэтому dy =
, поэтому dy = ![]() dt. Учитывая, что
dt. Учитывая, что ![]() = dx, получаем dy =
= dx, получаем dy = ![]() dx =
dx = ![]() (x)dx.
(x)dx.
Таким образом, дифференциал сложной функции y = f(x), где x = j(t), имеет вид dy = ![]() (x)dx, такой же, как в том случае, когда x является независимой переменной. Это свойство называется инвариантностью формы дифференциала.
(x)dx, такой же, как в том случае, когда x является независимой переменной. Это свойство называется инвариантностью формы дифференциала.