Определение. Многочленом степени ![]() называется выражение вида
называется выражение вида
![]() , где
, где ![]() ,
,![]() ,…,
,…,![]() - действительные числа,
- действительные числа, ![]() ,
,![]() .
.
Определение. Дробь вида ![]() , где
, где ![]() и
и ![]() – многочлены n-ой и m-ой степеней соответственно, называется рациональной дробью.
– многочлены n-ой и m-ой степеней соответственно, называется рациональной дробью.
Определение. Рациональная дробь называется правильной, если ![]() и неправильной, если
и неправильной, если ![]() .
.
Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби, поделив числитель на знаменатель. Поэтому интегрирование рациональных дробей сводится к интегрированию правильных рациональных дробей. А каждая правильная рациональная дробь представима в виде элементарных (простейших) рациональных дробей, т.е. дробей вида
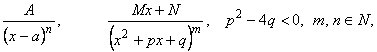
а их интегрирование производится следующим образом:
1) ![]()
2) ![]() .
.
3) ![]()


т.е. интеграл от элементарной рациональной дроби выражается через рациональные функции, логарифмы и арктангенсы.
Пример 2.13. Вычислить интеграл ![]()
Решение. Подынтегральная функция ![]() – неправильная рациональная дробь.
– неправильная рациональная дробь.
Разделим многочлен ![]() на многочлен
на многочлен ![]() столбиком
столбиком 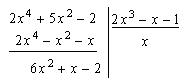
получим частное ![]() и остаток
и остаток ![]() , т.е. данная дробь представима в виде многочлена и правильной рациональной дроби:
, т.е. данная дробь представима в виде многочлена и правильной рациональной дроби:
![]()
Разложим многочлен ![]() на множители. Он имеет действительный корень
на множители. Он имеет действительный корень ![]() . Разделив
. Разделив ![]() на
на ![]() , получим
, получим
![]()
Квадратный трехчлен ![]() не имеет действительных корней, поэтому разложение, полученной правильной рациональной дроби, на элементарные дроби имеет вид
не имеет действительных корней, поэтому разложение, полученной правильной рациональной дроби, на элементарные дроби имеет вид
![]()
Методом неопределенных коэффициентов найдем А, М, N. Из равенства дробей следует равенство числителей
![]() ,
,
а многочлены равны, когда равны коэффициенты при одинаковых степенях

Решая систему, найдем ![]() таким образом
таким образом
![]()
и, следовательно,


 Пример 2.14. Вычислить
Пример 2.14. Вычислить ![]()
Решение. Разложим на простейшие дроби подынтегральную функцию, так как ![]() то
то ![]() Методом неопределенных коэффициентов найдем А и В
Методом неопределенных коэффициентов найдем А и В
![]() .
.
Пусть ![]() , тогда
, тогда ![]() пусть
пусть ![]() тогда
тогда ![]()
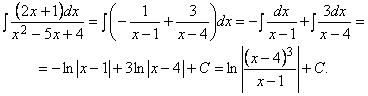
Пример 2.15. Вычислить ![]()
Решение. Знаменатель имеет двукратный корень ![]() и простой корень
и простой корень ![]() В этом случае разложение подынтегральной функции на простейшие дроби имеет вид
В этом случае разложение подынтегральной функции на простейшие дроби имеет вид
![]()
откуда ![]() или
или
![]()
сравнивая коэффициенты при одинаковых степенях ![]() , получим систему
, получим систему
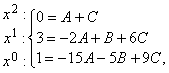
откуда находим ![]() следовательно
следовательно
![]()
![]()