При вычислении интегралов вида, где - рациональная функция от  и от . Покажем, что интеграл рационализируется подстановкой

,.

Действительно,

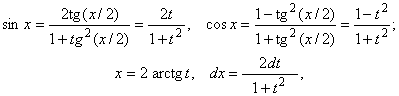
так что

где - рациональная функция от.

 -

При вычислении интегралов вида  от четной степени синуса или косинуса используются формулы понижения степени

При вычислении интегралов вида     от нечетной степени синуса или косинуса подынтегральную функцию нужно представить в виде

и ввести новую переменную  в первом и  – во втором интегралах.

При вычислении интегралов вида

применяют формулы тригонометрии

Пример 2.16. Найти

Решение.

Пример 2.17. Вычислить

Решение.  

Пример 2.18. Вычислить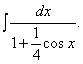

Решение. Применяя универсальную подстановку, получим