Пусть функция  определена на отрезке . Разобьем этот отрезок на  частей точками  .

 Определение. На каждом из частичных отрезков  возьмем произвольную точку  и составим сумму

  ,         (3.1)

которую назовем интегральной суммой для функции  на отрезке , соответствующей  данному разбиению  на частичные отрезки и данному выбору промежуточных  точек .

Геометрический смысл суммы очевиден: это сумма площадей прямоугольников с основаниями  и высотами (рис. 3.1 ) .

          Обозначим через  длину наибольшего частичного отрезка разбиения :

.

Определение. Если существует конечный предел I интегральной суммы (3.1) при

условии, что число частичных отрезков неограниченно увеличивается, а длина наибольшего из них стремиться к нулю, то этот предел называется определенным интегралом функции   по отрезку и обозначается

                                                 .                                         (3.2)

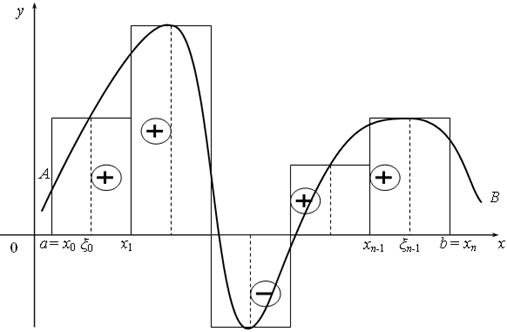
Рис. 3.1. Иллюстрация к понятию определенного интеграла функции

В этом случае функция  называется интегрируемой на .Числа  и  называются соответственно нижним и верхним пределами интегрирования, - подынтегральной функцией,  — переменной интегрирования.

    Сделаем ряд пояснений, так как имеет место не совсем обычный предельный переход. В самом деле, интегральная сумма зависит от точек разбиения ; и промежуточных точек  Число тех и дру­гих точек стремится к бесконечности при . Поэтому само понятие предела интегральной суммы требует уточнения. Сначала дадим соответствующее определение на «языке последовательностей». Пусть отрезок  по­следовательно разбивается на части сначала одним способом, затем — вторым, третьим и т. д., причем длина  наибольшего частичного отрезка - го разбие­ния стремится к нулю, когда  стремится к бесконечности. В каждом разбиении выберем произвольно промежуточные точки . Таким образом, по­лучаем последовательность раз­биений , у которой  и можно дать определение опре­деленного интеграла на «языке последовательностей»:

     Определение. Функция  называется интегрируемой на , если для любой последовательности разбиений , у которой , соответствующая последовательность интегральных сумм  стремится к одному и тому же числу I.

    Можно дать определение определенного интеграла и «на языке »:

Определение. Число I называется определенным интегралом от функции по отрезку, если для любого  существует  такое, что при  (т. е. если отрезок разбит на части с дли­нами ) независимо от выбора точек   выполняется неравенство

.

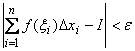 Доказательство эквивалентности обоих определений можно про­вести аналогично доказательству эквивалентности двух определе­ний предела функции. Определение «на языке последовательно­стей» дает возможность перенести основные понятия теории пре­делов и на этот новый вид предела.

Из определения определенного интеграла следует, что вели­чина интеграла (3.2) зависит только от вида функций  и от чисел  и . Следовательно, если заданы  и пределы интегрирования, то интеграл (3.2) определяется однозначно и представляет собой некоторое число. Отсюда, в частности, следует, что определенный интеграл не зависит от выбора обозначения для аргумента подынтегральной функции, т. е. от обозначения переменной интегрирования:

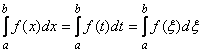               и т.д.