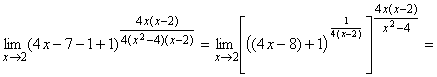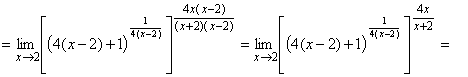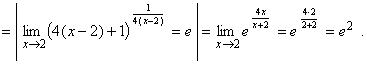При вычислении пределов следует помнить о типовых пределах, которые непосредственно можно получить из определений соответствующих функций.

1. , где f(x) – непрерывная в точке а функция, a – число.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Непосредственное применение теорем о пределах не всегда приводит к цели. Например, нельзя применить теорему о пределе дроби, если ее знаменатель стремится к нулю. Так, если числитель и знаменатель дроби   (при вычислении)  одновременно стремятся к нулю или к бесконечности, тогда говорят, что дробь представляет собой неопределенность типа  или . Чтобы найти предел такой дроби, надо раскрыть неопределенность. Для раскрытия неопределенности существует несколько стандартных приемов.

Пример 1. Вычислить  

Решение. Применяя основные теоремы о пределах, имеем

 .

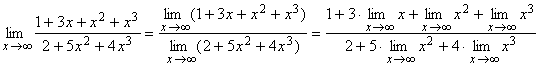Видно, что данная дробь представляет собой неопределенность типа , для раскрытия этой неопределенности преобразуем данную дробь, разделив числитель и знаменатель на старшую степень многочлена, в данном примере на , от этого величина дроби не изменится:

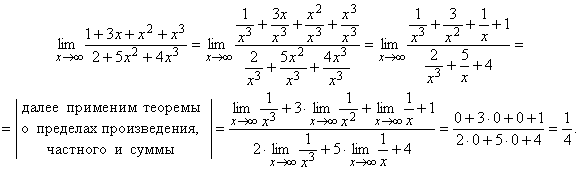
Таким образом, деление числителя и знаменателя дроби на старшую степень многочленов позволило от бесконечно больших величин перейти к бесконечно малым и тем самым раскрыть неопределенность.

Пример 2. Вычислить

Решение. Непосредственное применение теорем о пределе дроби приведет к неопределенности типа . Действительно, и числитель, и знаменатель стремятся к нулю при . Для раскрытия данной неопределенности избавимся от иррациональности в числителе дроби, для этого умножим числитель и знаменатель на выражение, сопряженное числителю, а именно на , в результате чего получим:

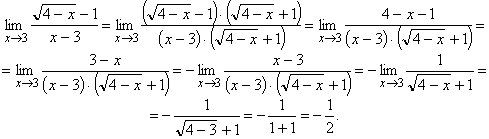
Итак, при наличии в дроби иррациональности  (если дробь представляет собой неопределенность типа ),  умножив числитель и знаменатель на сопряженное выражение, раскроем неопределенность.

Раскрытие неопределенности типа  возможно осуществлять и с помощью первого замечательного предела:  

Пример 3. Вычислить

Решение. Если подставить предельное значение, получим неопределенность типа . Применив формулы тригонометрии, преобразуем числитель и знаменатель дроби:  ,            ,  тогда

.

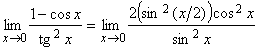Умножим и числитель, и знаменатель на , получим:

.

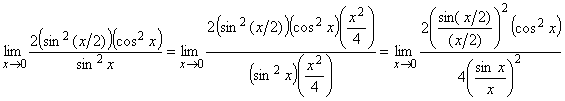Согласно первому замечательному пределу получим:

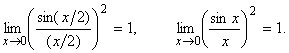
Следовательно,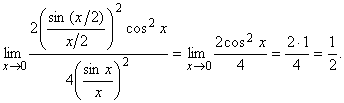 

Отметим, что при применении первого замечательного предела, бесконечно малая величина, стоящая под знаком синуса и в знаменателе должна быть одна и та же.

Помимо неопределенности типа  и , существуют неопределенности типа: 

Для раскрытия неопределенности  используют второй замечательный предел в одной из формулировок:

,   .

Пример  4. Вычислить следующие пределы:

а)  ;  б) .

а) 

б) Подставляя предельное значение, получаем неопределенность типа , преобразовав выражение под знаком предела, раскроем неопределенность. Для этого к выражению, стоящему в скобках, прибавим единицу и вычтем единицу. От этого выражение не изменится. Показатель степени умножим и разделим на  , получим: