Приближенное решение уравнения состоит из двух этапов:
1) отделения корней, то есть нахождения интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения (3.1).
2) уточнения корней до заданной точности.
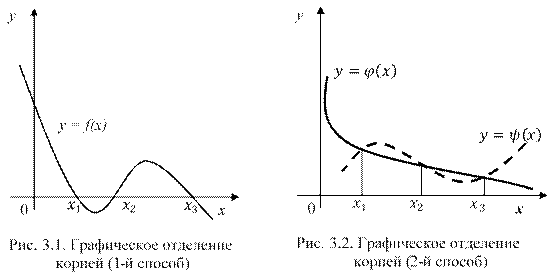
Отделение корней можно проводить графически и аналитически. Для того чтобы графически отделить корни уравнения (3.1), необходимо построить график функции y = f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения (рис. 3.1).
На практике же бывает удобнее заменить уравнение (3.1) равносильным ему уравнением:
![]() , (3.2)
, (3.2)
где ![]() ,
, ![]() – более простые функции, чем f(x).
– более простые функции, чем f(x).
Абсциссы точек пересечения графиков функций ![]() и
и ![]() дают корни уравнения (3.2), а значит и исходного уравнения (3.1) (рис. 3.2).
дают корни уравнения (3.2), а значит и исходного уравнения (3.1) (рис. 3.2).
 |
Аналитическое отделение корней основано на следующих теоремах:
 Теорема 1. Если непрерывная функция y = f(x) принимает на концах отрезка
Теорема 1. Если непрерывная функция y = f(x) принимает на концах отрезка ![]() значения разных знаков, т.е.
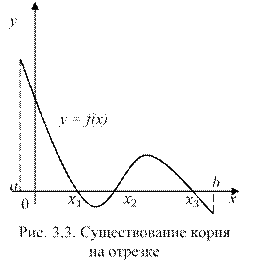
значения разных знаков, т.е. ![]() , то на этом отрезке содержится, по крайней мере, один корень уравнения (3.1) (рис. 3.3).
, то на этом отрезке содержится, по крайней мере, один корень уравнения (3.1) (рис. 3.3).
Теорема 2. Если непрерывная на отрезке ![]() функция y = f(x) принимает на концах отрезка значения разных знаков, а производная
функция y = f(x) принимает на концах отрезка значения разных знаков, а производная ![]() сохраняет знак внутри отрезка
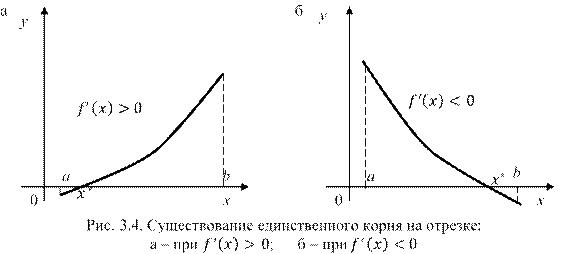
сохраняет знак внутри отрезка ![]() , то внутри отрезка существует единственный корень уравнения (рис. 3.4):
, то внутри отрезка существует единственный корень уравнения (рис. 3.4):
f(x) = 0.
 |
Уточнение корней до заданной точности заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Наиболее распространенными являются методы: деления отрезка пополам; касательных (Ньютона); секущих (хорд).