Основная задача интерполяции — нахождение значения таблично заданной функции в тех точках внутри данного интервала, где она не задана. Исходные табличные данные могут быть получены как экспериментально (в этом случае принципиально отсутствуют промежуточные данные без дополнительных работ), так и расчетным путем по сложным зависимостям (в этом случае найти с помощью интерполяции значение сложной функции бывает проще, чем непосредственным вычислением по сложной формуле)
Концепция интерполяции
Решение задач интерполяции и экстраполяции обеспечивается построением интерполяционной функции L(x), приближенно заменяющей исходную f(x), заданную таблично, и проходящей через все заданные точки — узлы интерполяции. С помощью этой функции можно рассчитать искомое значение исходной функции в любой точке.
В связи с интерполяцией рассматриваются три основные проблемы.
1) выбор интерполяционной функции L(x);
2) оценка погрешности интерполяции R(x);
3) размещение узлов интерполяции для обеспечения наивысшей возможной точности восстановления функции (x1, x2,…,xn).
Специальные методы интерполяции позволяют определить искомое значение функции без непосредственного прямого построения интерполяционной функции. В принципе все интерполяционные методы, базирующиеся на использовании в качестве интерполяционной функции полиномов, дают одни и те же результаты, но с разными затратами. Это объясняется тем, что полином n-й степени, содержащий n+1 параметр и проходящий через все заданные n+1 точки, — единственный. Кроме того, полином можно представить как усеченный ряд Тейлора, в который разложили исходную дифференцируемую функцию. Это, пожалуй, одно из главных достоинств полинома как интерполяционной функции. Поэтому чаще первая проблема интерполяции решается выбором в качестве интерполяционной функции именно полинома, хотя могут применяться и другие функции (например, тригонометрические полиномы, другие функции, выбранные из неформальных условий содержательной задачи).
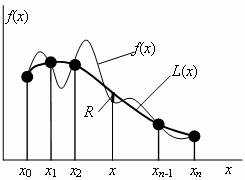
Рис. 3.2 Иллюстрация интерполяции
Выбор вида интерполяционной функции является в общем случае важной задачей, особенно если помнить, что через заданные точки можно провести любое количество функций (рис. 3.2). Следует отметить, что существует очевидный способ построения интерполяционной функции: из условия прохождения функции через все точки составляется система уравнений, из решения которой и находятся ее параметры. Однако этот путь далеко не самый эффективный, особенно при большом числе точек.
Принято различать локальную и глобальную интерполяцию. В том случае, когда полином един для всей области интерполяции, говорят, что интерполяция глобальная. В тех случаях, когда между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.
Линейная интерполяция
Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точки М(xi, yi) (i = 0, 1, …, n) соединяются прямолинейными отрезками, и функция f(x) приближается к ломаной с вершинами в данных точках (рис. 3.3).
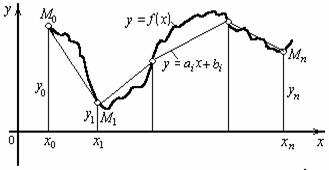
Рис. 3.3 Линейная интерполяция
Уравнения каждого отрезка ломаной линии в общем случае разные. Поскольку имеется n интервалов (xi , xi + 1), то для каждого из них в качестве уравнения
интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности, для i — го интервала можно написать уравнение прямой, проходящей через точки (xi , yi) и (xi + 1, yi + 1), в виде:
Отсюда
(3.2)
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (3.2) и найти приближенное значение функций в этой точке.
На рисунке 3.4 представлен пример использования линейной интерполяции в программе MathCAD. Для линейной интерполяции используется функция linterp(x,y,z). Здесь x, y – исходные данные, z – точка, в которой находится значение функции.
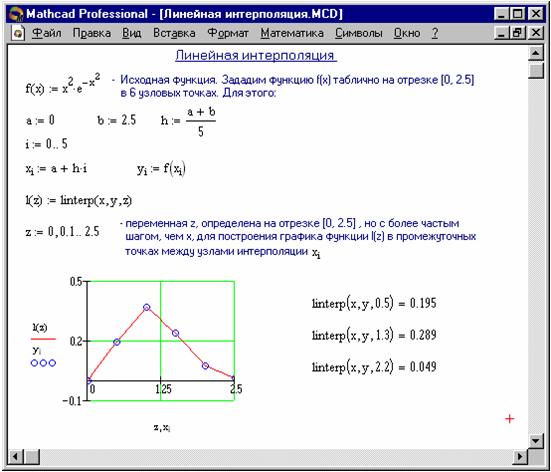
Рис. 3.4. Линейная интерполяция
Квадратичная интерполяция
В случае квадратичной интерполяции в качестве интерполяционной функции на отрезке (xi — 1,xi + 1) принимается квадратный трехчлен. Уравнения квадратного трехчлена имеет вид
y = aix2 + bix + ci,, xi — 1
x xi + 1, (3.3)
содержат три неизвестных коэффициента ai, bi, ci, для определения которых необходимы три уравнения. Ими служат условия прохождения параболы (3.3) через три точки (xi- 1, yi — 1), (xi, yi), (xi + 1, yi + 1). Эти условия можно записать в виде:
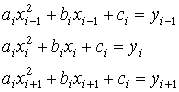
Интерполяция для любой точки x 
[x0, xn] проводится по трем ближайшим точкам.
Кубическая сплайн-интерполяция
В последние годы интенсивно развивается новый раздел современной вычислительной математики — теория сплайнов. Сплайны позволяют эффективно решать задачи обработки экспериментальных зависимостей между параметрами, имеющих достаточно сложную структуру.
Рассмотренные выше методы локальной интерполяции, по существу, является простейшим сплайном первой степени (для линейной интерполяции) и второй степени (для квадратичной интерполяции).
Наиболее широкое практическое применение, в силу их простоты, нашли кубические сплайны. Основные идеи теории кубических сплайнов сформировались в результате попыток математически описать гибкие рейки из упругого материала (механические сплайны), которыми издавна пользовались чертежники в тех случаях, когда возникала необходимость проведения через заданные точки достаточно гладкой кривой. Известно, что рейка из упругого материала, закрепленная в некоторых точках и находящаяся в положении равновесия, принимает форму, при которой ее энергия является минимальной. Это фундаментальное свойство позволяет эффективно использовать сплайны при решении практических задач обработки экспериментальной информации.
В общем случае для функции y = f(x) требуется найти приближение y= j(x) таким образом, чтобы f(xi) = j(xi) в точках x = xi, a в остальных точках отрезка [a, b] значения
функций f(x) и j(x) были близкими между собой. При малом числе экспериментальных точек (например, 6-8) для решения задачи интерполяции можно использовать один из методов построения интерполяционных полиномов. Однако при большом числе узлов интерполяционные полиномы становятся практически непригодными. Это связано с тем, что степень интерполяционного полинома лишь на единицу меньше числа экспериментальных значений функций. Можно, конечно, отрезок, на котором определена функция, разбить на участки, содержащие малое число экспериментальных точек, и для каждого из них построить интерполяционные полиномы. Однако в этом случае аппроксимирующая функция будет иметь точки, где производная не является непрерывной, т. е. график функции будет содержать точки “излома”.
Кубические сплайны лишены этого недостатка. Исследования теории балок показали, что гибкая тонкая балка между двумя узлами достаточно хорошо описывается кубическим полиномом, и поскольку она не разрушается, то аппроксимирующая функция должна быть, по меньшей мере, непрерывно дифференцируемой. Это означает, что функции j(x), j’(x), j»(x) должны быть непрерывными на отрезке [a, b].
Кубическим интерполяционным сплайном, соответствующим данной функции f(x) и данным узлам xi, называется функция y(x), удовлетворяющая следующим условиям:
1. на каждом сегменте [xi — 1, xi], i = 1, 2, ..., n функция y(x) является полиномом третьей степени,
2. функция y(x), а также ее первая и вторая производные непрерывны на отрезке [a,b],
Кубический сплайн склеивается из полиномов третьей степени, которые для i-го участка записываются так:
Для всего интервала будет соответственно п кубических полиномов, отличающихся коэффициентами аi, bi, ci, di. Чаще всего узлы при сплайновой интерполяции располагают равномерно, т.е. хi+1 -хi =const = h (хотя это и необязательно).
Необходимо найти четыре коэффициента при условии прохождения каждого полинома через две точки (xi, yi) и (xi+1, yi+1) , следствием чего являются следующие очевидные уравнения:
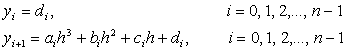
Первое условие соответствует прохождению полинома через начальную точку, второе — через конечную точку. Найти все коэффициенты из этих уравнений нельзя, так как условий меньше, чем искомых параметров. Поэтому указанные условия дополняют условиями гладкости функции (т.е. непрерывности первой производной) и гладкости первой производной (т.е. непрерывности второй производной) в узлах интерполяции. Математически эти условия записываются как равенства соответственно первой и второй производных в конце i-го и в начале (i+1)-го участков.
Так как 
и 
, то
(y’(xi+1) в конце i-го участка равна у’ (хi+1) в начале (i+1)-го),
( у» (хi+1) в конце i-го участка равна у» (хi+1) в начале (i+1)-го).
Получилась система линейных уравнений (для всех участков), содержащая 4n — 2 уравнения с 4n неизвестными (неизвестные a1, a2,…, an, b1,…, dn — коэффициенты сплайнов). Для решения системы добавляют два граничных условия одного из следующих видов (чаще применяют 1):
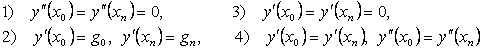
Совместное решение 4n уравнений позволяет найти все 4n коэффициента.
Для восстановления производных можно продифференцировать на каждом участке соответствующий кубический полином. В случае необходимости определения производных в узлах существуют специальные приемы, сводящие определение производных к решению более простой системы уравнений относительно искомых производных второго или первого порядка. К важным достоинствам интерполяции кубическими сплайнами относится получение функции, имеющей минимальную возможную кривизну. К недостаткам сплайновой интерполяции относится необходимость получения сравнительно большого числа параметров.
Решим задачу об интерполяции с помощью программы MathCAD. Для этого воспользуемся встроенной функцией interp(VS,x,y,z). Переменные x и y задают координаты узловых точек, z является аргументом функции, VS определяет тип
граничных условий на концах интервала.
Определим интерполяционные функции для трех типов кубического сплайна
Здесь cspline(VX, VY) возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;
pspline(VX, VY) возвращает вектор VS вторых производных при приближении к опорным точкам к параболической кривой;
lspline(VX, VY) возвращает вектор VS вторых производных при приближении к опорным точкам прямой;
interp(VS, VX, VY, x) возвращает значение y(x) для заданных векторов VS, VX, VY и заданного значения x.
Вычисляем значения интерполяционных функций в заданных точках и сравниваем результаты с точными значениями
Обратите внимание, что результаты интерполяции различными типами кубических сплайнов практически не отличаются во внутренних точках интервала и совпадают с точными значениями функции. Вблизи краев интервала отличие становится более заметным, а при экстраполяции за пределы заданного интервала различные типы сплайнов дают существенно разные результаты. Для большей наглядности представим результаты на графике (рис. 3.5)
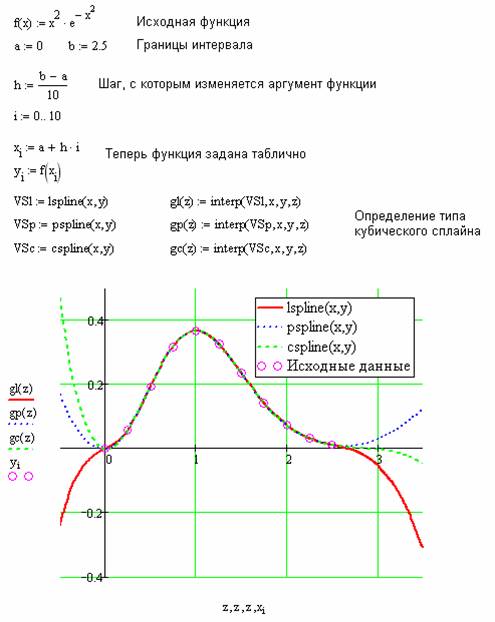
Рис. 3.5 Кубическая сплайн интерполяция
Если функция задана дискретно, то для интерполяции задаются матрицы данных.
При глобальной интерполяции наиболее часто используется интерполяция полиномом n-ой степени или интерполяция Лагранжа.
Классический подход основывается на требовании строгого совпадения значений f(х) и j(х) в точках хi (i = 0, 1, 2, … n).
Будем искать интерполяционную функцию j(х) в виде полинома степени n.
Этот полином имеет n + 1 коэффициент. Естественно предположить, что n + 1 условий
j(x0) = y0, j(x1) = y1, . . ., j(xn) = yn (3.4)
наложенные на полином
(3.5)
позволяют однозначно определить его коэффициенты. Действительно, требуя для j(х) выполнение условий (3.4), получаем систему n + 1 уравнений с n + 1 неизвестными:
(3.6)
Решая эту систему относительно неизвестных a0, a1, …, an мы получим аналитическое выражение полинома (3.5). Система (3.6) всегда имеет единственное решение, т.к. её определитель
известный в алгебре как определитель Вандермонда, отличен от нуля. Отсюда следует, что интерполяционный полином j(х) для функции f(х), заданной таблично, существует и единственен.
Полученное уравнение кривой проходит точно через заданные точки. Вне узлов интерполяции математическая модель может иметь значительную погрешность
Интерполяционная формула Лагранжа
Пусть известны значения некоторой функции f(х) в п+1 различных произвольных точках yi = f(xi), i = 0,…, п. Для интерполирования (восстановления) функции в какой-либо точке х, принадлежащей отрезку [х0,хп], необходимо построить интерполяционный полином n-го порядка, который в методе Лагранжа представляется следующим образом:
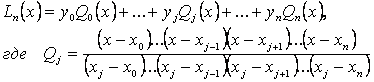
Причем нетрудно заметить, что Qj(xi) = 0, если i¹j, и Qj(xi) =1, если i=j. Если раскрыть произведение всех скобок в числителе (в знаменателе все скобки — числа), то получим полином n-го порядка от х, так как в числителе содержится n сомножителей первого порядка. Следовательно, интерполяционный полином Лагранжа не что иное, как обычный полином n-го порядка, несмотря на специфическую форму записи.
Оценить погрешность интерполяции в точке х из [х0,хn] (т.е. решить вторую
проблему интерполяции) можно по формуле
В формуле 
— максимальное значение (n+1)-й производной исходной функции f(х) на отрезке [х0,хn]. Следовательно, для того чтобы оценить погрешность интерполяции, необходима некоторая дополнительная информация об исходной функции (это должно быть понятно, так как через заданные исходные точки может проходить бесчисленное количество различных функций, для которых и погрешность будет разной). Такой информацией является производная n+1 порядка, которую не так просто найти. Ниже будет показано, как выйти из такого положения. Отметим также, что применение формулы погрешности возможно, только если функция дифференцируема n +1 раз.
Для построения интерполяционной формулы Лагранжа в MathCAD удобно использовать функцию if.
if (cond , х , у )
Возвращает значение х, если cond отличен от 0 (истина). Возвращает значение у, если cond равен 0 (ложь) (рисунок 3.6).