Метод простых итераций во всех рассмотренных вариантах использует для построения очередного приближения  только информацию о функции в одной лишь точке ; при этом никак не используются предыдущие значения  Однако эту предыдущую информацию также можно использовать при нахождении . В качестве примера рассмотрим нахождение  по двум предыдущим приближениям  и  с помощью линейной интерполяции. Этот метод называется методом хорд.

Идея метода состоит в том, что по двум точкам  и  построить прямую  (то есть хорду, соединяющую две точки графика  ) и взять в качестве следующего приближения  абсциссу точки пересечения этой прямой с осью Ox. Иными словами, необходимо приближённо заменить на этом шаге функцию f(x) её линейной интерполяцией, найденной по двум значениям x:  и .

Линейной интерполяцией функции f(x) назовём такую линейную функцию l(x), значения которой совпадают со значениями f(x)в двух фиксированных точках, в данном случае в точках  и .

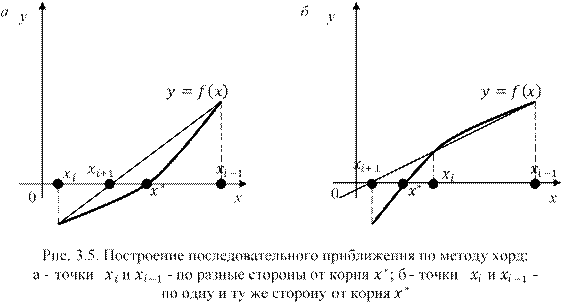
В зависимости от того, лежат ли точки   и  по разные стороны от корня  или же по одну и ту же сторону, рассматриваем два случая (рис. 3.5).

Итак, очередное последовательное приближение будет зависеть от двух предыдущих:

 .

Найдём выражение для функции .

Интерполяционную линейную функцию  будем искать как функцию с угловым коэффициентом, равным разностному отношению:

,

построенному для отрезка между  и , график которой проходит через точку :

Решая уравнение , находим:

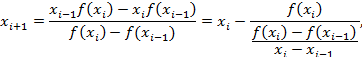
то есть

.                                                      (3.3)

Заметим, что величина может рассматриваться как разностное приближение для производной  в точке . Таким образом, полученная формула (3.3) – это разностный аналог итерационной формулы метода Ньютона.

Вычисление по формуле (3.3) гораздо предпочтительнее вычисления по другой полученной нами формуле:

хотя эти две формулы математически тождественны, поскольку при использовании формулы (3.3) в случае вычислений с округлениями (например на компьютере) достигается меньшая потеря значащих цифр.

Вычисления ведутся непосредственно по формуле (3.3) при , начиная с двух приближений  и , взятых, по возможности, поближе к корню . При этом не предполагается, что  лежит между  и  (и что значения функции f( в точках  и  имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между   и  на каком-либо следующем шаге (хотя это и не исключено). В таком случае затруднительно дать оценку погрешности, с которой   приближает истинное значение корня  Поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство:

 ,

где  –  желаемая точность нахождения корня. При этом полагают приближённое значение корня равным:

.

Пример 1

Решить методом хорд нелинейное уравнение ,

Решение

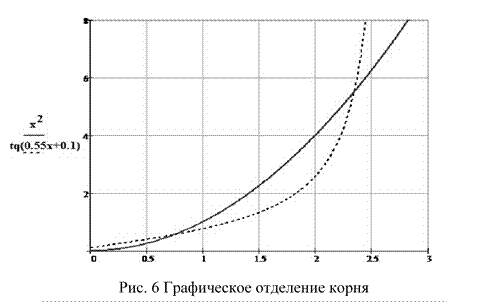
Определим корень графически. Построим графики функций (рис. 3.6):

 и ,

составив таблицы значений этих функций (табл. 3.1, 3.2):

Таблица 3.1

x	y2 = x2	0,55x	y1
0	0	0	0,
0,2	0,04	0,1	0,21
0,4	0,16	0,22	0,33
0,6	0,36	0,33	0,46
0,8	0,64	0,44	0,60
1	1	0,55	0,76

Таким образом, положительный корень уравнения заключён в промежутке

Чтобы уточнить корень методом хорд, определим знак функции

на концах промежутка [0.6; 0.8] и знак её второй производной в этом промежутке:

;

Для вычислений применяем формулу (3.3):

,

Вычисления удобно располагать в таблицах (табл. 3.2, 3.3).

Таблица 3.2

n
0	0,6	0,2	0,43	0,4586
1	0,748	0,058	0,5081	0,5570
2	0,750	0,50	0,5125	0,5627
3	0,7502	0,0498	0,5126	0,5628

Таблица 3.3

n
0	0,36	0,0986	-0,1392	-0,142
1	0,5506	0,0064	-0,0470	-0,008
2	0,5625	0,0002	-0,0408	-0,0002
3	0,5628	0

Ответ:          x = 0,750.

Пример 2

Решить методом хорд нелинейное уравнение 

Решение

Отделим корни уравнения аналитически. Находим:

Составим таблицу знаков функции f(x):

Таблица 3.4

Signf(x)	-	-	+	+

Уравнение имеет один действительный корень, лежащий в промежутке [-1,0]. Чтобы уточнить корень, находим вторую производную:

;

в промежутке    [-1;0] выполняется неравенство

Для вычисления  применим формулу:

где

Вычисления располагаем в таблицах (табл. 3.5, 3.6).

Таблица 3.5

0	0	0	0	0	0
1	-0,882	-0,6861	0,7779	0,1556	-0,441
2	-0,943	-0,8386	0,8892	0,1778	-0,4715
3	-0,946	-0,8466	0,8949	0,1790	-0,473
4	-0,946

Таблица 3.6

0	1,5	1,7	1	-0,118
1	0,2173	0,4173	0,118	-0,057
2	0,0121	0,2121	0,057	-0,054
3	0,0014	0,2014	0,054	-0,054