Определение. Пусть функция  ограничена на отрезке  и - разбиение этого отрезка точками . Обозначим через  и   соответственно  точную нижнюю и точную верхнюю грани этой функции на отрезке  и составим следующие суммы:

,

.

Эти суммы называются соответственно верхней  и нижней суммами или верхней  и нижней суммами Дарбу функции  для данного разбиения  отрезка .

Из определения  нижней и верхней граней следует, что  при

. Отсюда

,

т.е. любая интегральная сумма  и суммы Дарбу для данного разбиения связаны неравенствами

.

Суммы Дарбу имеют простой геометрический смысл. Рассмотрим неотрицательную непрерывную  функцию на  и  криволинейную трапецию, т. е. фигуру, ограниченную графиком функции, двумя вертикальными прямыми, проведенными через   точки и  оси , и осью  (рис. 3.2 и 3.3). Поскольку функция непрерывна на , она непрерывна и на . По второй теореме Вейерштрасса функция  достигает на  своих точных граней, и, следовательно,  и  - соответственно наименьшее и наибольшее значения функции на этом отрезке. Поэтому сумма S равна площади заштрихованной на рис. 3.2 ступенчатой фигуры, «описанной» около криволинейной трапеции, а сумма  равна площади заштрихованной на рис. 3.3 ступенчатой фигуры, «вписанной» в данную криволинейную трапецию.

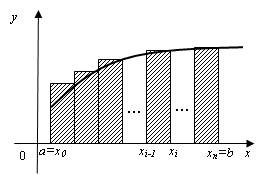
Рис. 3.2. Геометрический смысл нижней суммы Дарбу

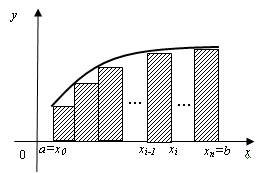
Рис. 3.3. Геометрический смысл верхней суммы Дарбу

Следует особо отметить, что суммы Дарбу зависят только от разбиения отрезка , в то время как интегральная сумма  зависит еще и от выбора точек  на частичных отрезках . При фиксированном разбиении отрезка  суммы  и - некоторые числа, а сумма - переменная величина, так как точки  произвольны.