Если функция 
непрерывна на отрезке 
и для нее известен неопределенный интеграл 
, где 
– какая либо первообразная функции , то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница
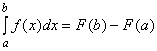, (3.10)
т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
При вычислениях формулу (3.10) обычно записывают в виде
,
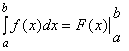где символ в правой части равенства – "подстановка от 
до 
" – обозначает ту же самую разность 
.
Пример 3.1. Вычислить интеграл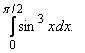 
Решение.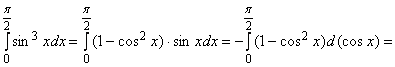 
.
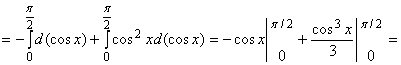
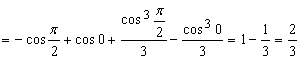