Основные правила нахождения производной
1) Если 
, то 
.
2) 
, где .
3) 
.
4) 
.
5) 
.
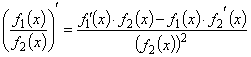6) Если 
и 
, то 
(производная обратной функции).
7) Если 
, то 
, 
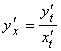(производная параметрически заданной функции).
8) Если имеется сложная функция 
, то 
(производная сложной функции).
9) Если переменные 
и 
связаны функциональным соотношением 
, так, что не выражено явно через , тогда находят производные левой и правой части равенства 
по отдельности, учитывая, что зависит от и, приравнивая производные, получают новое равенство, из которого определяется 
(производная неявной функции).
Таблица производных основных элементарных функций:
|
1. 2. 3. 4. 5. 6. |
7. 8. 9. 10. 11. |
12. 13. 14. 15. 16. 17. |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.Пример 1. Найти производную функции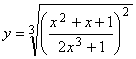 
.
Решение.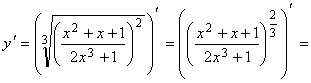 
.
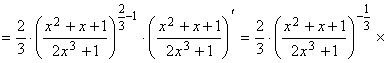
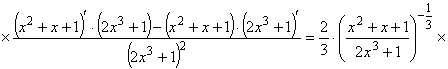
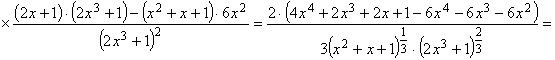
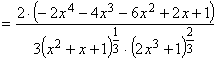Пример 2. Найти производную функции 
.
Решение. 
.
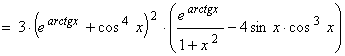Пример 3. Найти производную функции
.
Решение. 
.
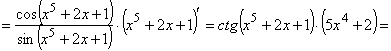
Пример 4. Найти 
.
Решение. Чтобы найти производную функции типа 
, поступают так:
вначале логарифмируют данное равенство
,
затем находят производные от обеих частей полученного равенства, приравнивая их:
.
Получают:
,
или
.
Учитывая, что 
, имеем:
.
Дифференцируя это равенство, получаем:
; 
;
; 
.
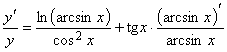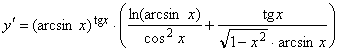Пример 5. Найти 
, если переменные 
и 
связаны соотношением:
.
Решение. Явно выразить одну из переменных через другую невозможно, поэтому находим производные левой и правой частей данного равенства и приравниваем их:
,
далее имеем:
;
.
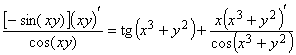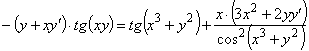Перенося слагаемые, содержащие 
, в одну часть равенства (вынося за скобку), а остальные слагаемые – в другую и деля на коэффициент при , получаем:
.
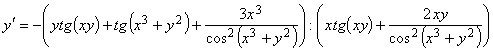Вторая производная функции – это производная от первой производной: 
, и вообще, 
-я производная – это производная от 
-й производной, а именно:
.
Пример 6. Найти 
и 
для функции 
.
Решение
.
.
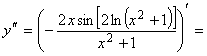
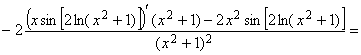
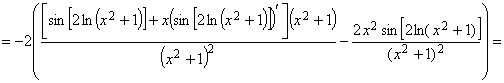
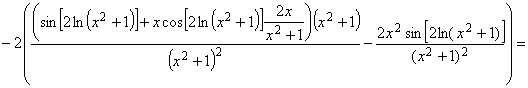
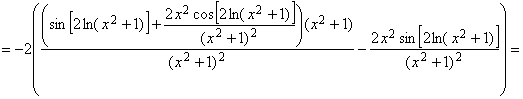
Для случая параметрического задания функции 
, имеем:
, 
.
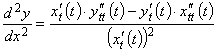Пример 7. Найти 
и 
для функции, заданной параметрически:
.
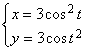Решение
; 
;
; 
;
;
.
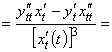