Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка

                   (3.8)

Основная задача, для решения в которой используют уравнению (3.8), называется задачей Коши. Её решение имеет вид:

                     (3.9)

и удовлетворяет начальному условию

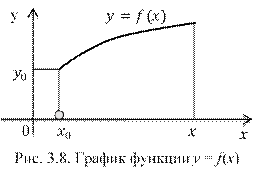
Иными словами, требуется найти интегральную кривую , проходящую через заданную точку  (рис. 3.8).

Если правая часть  непрерывна в области R, определяемой неравенствами

то существует, по меньшей мере, одно решение (3.9), определенное в некоторой окрестности:

,

где h – положительное число. Это решение единственно, если в области R выполнено условие Липшица

,                                    (3.10)

где N – постоянная (константа Липшица), зависящая в общем случае от а и b.

Если  имеет ограниченную производную в области  то можно положить:

              при            р.

Для дифференциального уравнения n-го порядка

задача Коши состоит в нахождении решения , удовлетворяющего начальным условиям