Пусть дано дифференциальное уравнение
(3.22)
с начальным условием:
.
Выбрав достаточно малый шаг 
, постоим систему равноотстоящих друг от друга точек:
(3.23)
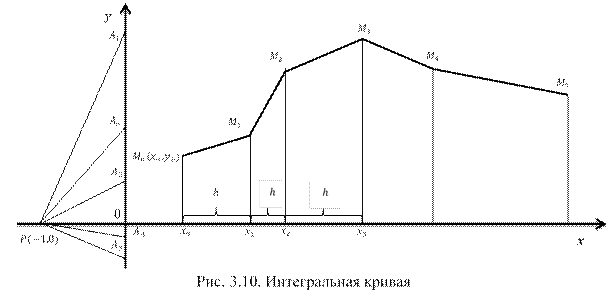Искомую интегральную кривую 
(рис. 3.10), проходящую через точку 
, приближенно заменим ломаной 
с вершинами 
, звенья которой 
прямолинейны между прямыми 
и 
и имеют подъем:
(3.24)
(это так называемая ломаная Эйлера).
Таким образом, звенья ломаной Эйлера в каждой вершине 
имеют направление 
, совпадающее с направлением интегральной кривой уравнения (3.22), проходящей через точку .
Из формулы (3.24) вытекает, что значения 
могут быть определены (метод Эйлера) по формулам:
(3.25)
Для геометрического построения ломаной Эйлера выберем полюс 
и на оси ординат отложим отрезок 
(см. рис. 3.10).
Очевидно, угловой коэффициент луча 
будет равен 
. Поэтому, чтобы получить первое звено ломаной Эйлера, достаточно из точки 
провести прямую
, параллельную лучу 
, до пересечения с прямой 
в некоторой точке 
.
Приняв точку 
за исходную, откладываем на оси ординат отрезок 
и через точку 
проводим прямую 
до пересечения в точке 
с прямой 
и т.д.
Метод Эйлера является простейшим численным методом интегрирования дифференциального уравнения. Недостатками метода Эйлера являются:
1) малая точность;
2) систематическое накопление ошибок.
Можно доказать, что если правая часть 
уравнения (3.22) непрерывна, то последовательность ломаных Эйлера про 
на достаточно малом отрезке
равномерно стремится к искомой интегральной кривой 
.
Метод Эйлера легко распространяется на системы дифференциальных уравнений