Часто для вычисления интеграла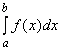 
полезно заменить переменную интегрирования 
новой переменной 
при помощи подстановки 
или 
. При этом необходимо перейти от старых пределов интегрирования 
и 
к новым пределам 
и 
которые определяют из уравнений 
, 
или 
Замена переменной осуществляется по формуле
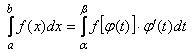(3.11)
Эта формула справедлива, если 
– непрерывная функция, а функция 
сама непрерывна и имеет непрерывную производную на отрезке 
.
При вычислении определенного интеграла методом замены переменной возврат к старой переменной не требуется.
Пример 3.2. Вычислить интеграл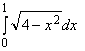 
.
Решение. Положим 
, тогда 
. Такая подстановка возможна (так как при любом значении 
под корнем получается неотрицательная величина) и приводит к тому, что корень под знаком интеграла исчезает. При этом изменению переменной 
от 
до 
соответствует изменение переменной от 
до 
. Применяя формулу (3.11) получаем
.
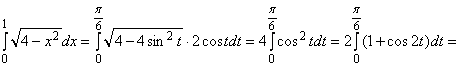
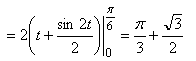Пример 3.3. Вычислить интеграл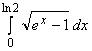 
.
Решение. Положим 
, тогда ex – 1 = t2, ex = t2 + 1, дифференцируем обе части равенства: exdx = 2tdt, откуда 
.
При x = 0: 
;
при x = ln2: 
,
поэтому
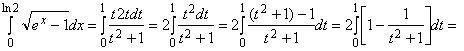
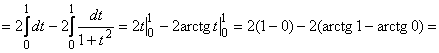
