Если функции  v(x)  и  u(x) обладают непрерывными производными на отрезке   [a, b], то справедлива формула интегрирования по частям для определенного интеграла

                  (3.12)

Замечание. Некоторые часто встречающиеся интегралы, которые вычисляются методом интегрирования по частям, указаны в гл. 2, пп. 2.7, с. 30 необходимо в них только расставить пределы интегрирования.

Пример 3.4. Вычислить интеграл  .

Решение.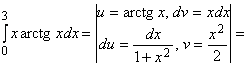

.

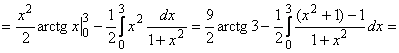
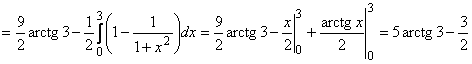Пример 3.5. Вычислить интеграл  .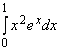

Решение.

.
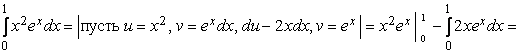
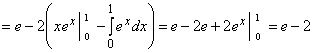