Пример 1. Найти наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке ![]() .
.
Решение. Найдем критические точки (подозрительные на экстремум) функции из условия, что ![]() или
или ![]() не существует:
не существует:
![]() ,
,
![]() во всех точках существует,
во всех точках существует, ![]() , когда
, когда ![]() .
.
Раскладывая левую часть на множители, получаем:
![]() ,
,
отсюда находим критические точки: ![]() ,
, ![]() ,
, ![]() .
.
Из этих точек отрезку ![]() принадлежат только две:
принадлежат только две: ![]() и
и ![]() . Найдем значение функции в этих точках и на концах отрезка, т.е. при
. Найдем значение функции в этих точках и на концах отрезка, т.е. при ![]() и
и ![]() :
:
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Итак, получили ![]() ,
, ![]() .
.
Пример 2. Найти наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке ![]() .
.
Решение. ![]() ,
, ![]() определена во всех точках;
определена во всех точках; ![]() при
при ![]() . На отрезке
. На отрезке ![]()
![]() при
при ![]() .
.
Имеем три точки: ![]() ,
, ![]() ,
, ![]() , в которых могут достигаться наибольшее и наименьшее значения.
, в которых могут достигаться наибольшее и наименьшее значения.
![]() ;
; ![]() ;
;
![]() .
.
Итак, ![]() ,
, ![]() .
.
Среди многих применений производной функции одного переменного важное значение имеет решение так называемых задач на максимум (минимум).
Пример 3. Найти прямоугольный треугольник наибольшей площади, у которого сумма катета и гипотенузы равна ![]() .
.
Решение. Обозначим один из катетов треугольника через ![]() , тогда гипотенуза будет равна
, тогда гипотенуза будет равна ![]() , а другой катет, по теореме Пифагора будет равен:
, а другой катет, по теореме Пифагора будет равен:
![]() .
.
Площадь треугольника ![]() , так как
, так как ![]() должна быть максимальной, то
должна быть максимальной, то ![]() или
или ![]() не существует. Находим производную:
не существует. Находим производную:
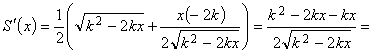
![]() .
.
![]() не существует, если
не существует, если ![]() , но тогда катет окажется равным гипотенузе, что невозможно.
, но тогда катет окажется равным гипотенузе, что невозможно. ![]() , если
, если ![]() . Тогда
. Тогда ![]() , гипотенуза будет равна
, гипотенуза будет равна ![]() ; т.е.
; т.е. ![]()
![]() , где
, где ![]() – угол, прилежащий к катету
– угол, прилежащий к катету ![]() . Значит,
. Значит, ![]() ; другой угол будет
; другой угол будет ![]() . В этой точке:
. В этой точке:
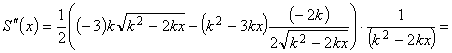
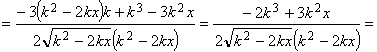
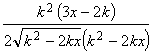 ,
,
при ![]() имеем:
имеем: 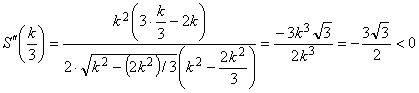 , значит, это действительно точка максимума.
, значит, это действительно точка максимума.
Искомый треугольник – это прямоугольный треугольник с углами ![]() ,
, ![]() и сторонами
и сторонами ![]() ,
, ![]() и
и ![]() .
.
Пример 4. Из трех одинаковых досок изготовить симметричный желоб с наибольшей площадью поперечного сечения.
Решение. Ширину данных досок обозначим через ![]() . Поперечное сечение изображено на рис. 3. 1.
. Поперечное сечение изображено на рис. 3. 1.
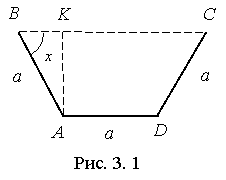 Обозначим через
Обозначим через ![]() угол
угол ![]() (
(![]() ), тогда
), тогда ![]() ,
, ![]() .
.
Площадь поперечного сечения (площадь трапеции) будет:
![]()
![]() .
.
Наибольшее значение эта функция принимает в точке максимума, а необходимым условием того, что точка ![]() является точкой максимума функции
является точкой максимума функции ![]() , является то, что
, является то, что ![]() или
или ![]() не существует. Найдем точку максимума:
не существует. Найдем точку максимума:
![]() ,
,
но ![]() всегда существует. Точки, в которых
всегда существует. Точки, в которых ![]() , находятся из уравнения:
, находятся из уравнения: ![]() . Тогда
. Тогда ![]() или
или ![]() . Если
. Если ![]() , то
, то ![]() , но в этом случае никакого желоба не получится, так как
, но в этом случае никакого желоба не получится, так как ![]() . Остается случай, когда
. Остается случай, когда ![]() , тогда
, тогда ![]() , так как
, так как ![]() .
.
Проверим, является ли эта точка точкой максимума ![]() . Найдем
. Найдем ![]() :
:
![]()
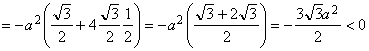 .
.
Значит, ![]() действительно точка максимума:
действительно точка максимума:
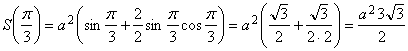 .
.