Формулировка задачи

Пусть некоторый полуфабрикат (например, листы фанеры или рулоны бумаги) поступил на предприятие в виде  партий, содержащих  единиц полуфабрикатов одинакового для каждой партии размера. Из поступивших полуфабрикатов требуется изготовить возможно большее количество комплектов деталей в каждый из которых входит  деталей 1-го вида,  деталей 2-го вида, … ,  деталей s-го вида.

Пусть каждую единицу полуфабриката можно раскроить на детали  различными способами, причем при раскрое -й партии, -м способом получается  деталей -го вида .

Математическая постановка

Обозначим через  число единиц из -й партии полуфабрикатов, которые намечено раскроить -м способом, так что из -й партии при -м способе раскроя будет получено  деталей -го вида. Всего из всей -й партии деталей -го вида будет получено , а из всех  партий их будет получено: .

Так как в каждый комплект должно входить  деталей -го вида, то  деталей позволит их использовать для составления 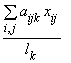 комплектов, и, таким образом, число полных комплектов, которое можно выпустить по данному плану , будет равно:

.

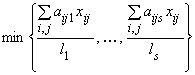Введем дополнительную переменную  – отходы при используемом способе раскроя. В результате, получим задачу линейного программирования:

,

при ограничениях

       ,

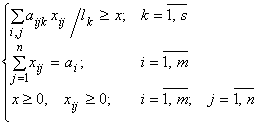где ,  целые числа. Здесь  + 1 неотрицательных неизвестных,  ограничений-неравенств и  ограничений-равенств, целевая функция зависит от одной переменной.