Схема 1.

1) Разбиваем величину  u   на большое число n малых слагаемых Δu_i

                                              u = Δ u₁  + Δ u₂+…+Δ u_n = .

2) Выражаем    приближенно   каждое   слагаемое  Δu_i   в  виде       произведения

Δu_i = f(x_i)Δx_i, где  f(x_i)  – данная   или       определяемая     из    условия   задачи функция,

 x₀= a , x₁ , x₂,…, x_n = b – точки отрезка , которые разбивают его на n равных частей.

3) Представляем приближенное значение u в виде интегральной суммы

u = .

Если из условия задачи следует, что погрешность этого приближенного равенства стремится к нулю при n , то искомая величина  выражается определенным интегралом:

 .

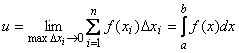Схема 2.

1) Пусть величина u получает приращение Δ u = f(x)Δx  соответствующее изменению x  на малую величину Δx; f(x)  рассматривается как данная или определяемая из условия задачи функция от  x.

2) Заменив приращение Δu дифференциалом (главная часть приращения Δu ) и  Δx – дифференциалом  dx (Δx = dx), получим du = f(x)dx .

3) Интегрируя это равенство в пределах от  x = a   до  x = b, получим 

.
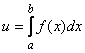