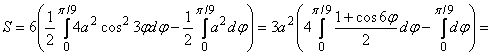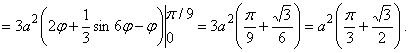1. Если непрерывная кривая задана в прямоугольных координатах уравнением , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальными прямыми  и отрезком оси Оx  (рис. 3.5) определяется по формуле

.

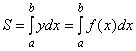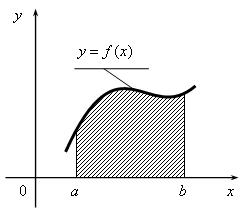
Рис. 3.5. Пример криволинейной трапеции, ограниченной осью Ох

В более общем случае, если криволинейная трапеция ограничена и сверху и снизу непрерывными кривыми (рис. 3.6), уравнения которых

,

то рассматривая криволинейную трапецию CDEF как разность двух фигур ADEB и ACFB получим формулу

.

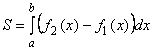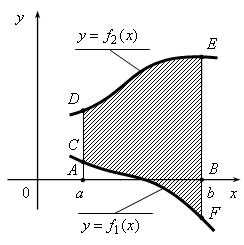
Рис. 3.6. Общий вид криволинейной трапеции

2. Если линия задана параметрическими уравнениями , то формула будет иметь вид

,

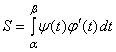где  – значения, между которыми изменяется параметр t, когда точка пробегает слева направо всю линию, ограничивающую трапецию сверху.

3. Пусть дан сектор OAB, ограниченный дугой АВ и двумя радиус-векторами ОА и ОВ (рис. 3.7). При этом дуга АВ задана в полярной системе координат уравнением , где  – положительная, непрерывная на отрезке  функция. Тогда площадь сектора АОВ вычисляется по формуле

.

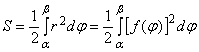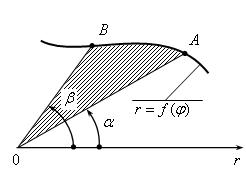
Рис. 3.7. Определение площади сектора

Пример 3.6. Вычислить площадь фигуры, заключенной между кривой , осью OX и прямой .

Решение. Построим данную криволинейную трапецию (рис. 3.8) и вычислим ее площадь

.

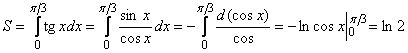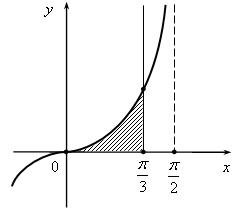
Рис. 3.8. Пример криволинейной трапеции

Пример 3.7. Вычислить площадь фигуры, ограниченной параболами .

Решение. Решая систему уравнений

 ,

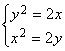находим абсциссы точек пересечения парабол  и значит

.

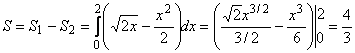Пример 3.8. Вычислить площадь эллипса .

Решение. Здесь удобнее записать параметрические уравнения эллипса, которые имеют вид . Вычислим площадь верхней половины эллипса и удвоим ее. Учитывая, что при возрастании переменной x от (- а) до a, параметр t убывает от  до 0, получим

.

Пример 3.9. Найти площадь фигуры, ограниченной кривой , лежащей вне круга  (рис. 3.9).

Рис. 3.9. Иллюстрация к примеру 3.9

Решение. Учитывая симметрию кривой, решаем совместно уравнения трехлепестковой розы и окружности. Находим полярный угол точки их пересечения в первой четверти

 ,    , 

 ,  .

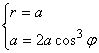Таким образом, площадь фигуры будет равна