1. Площадь поверхности, образованной вращением вокруг оси Ox дуги гладкой кривой ![]() , заключенной между точками с абсциссами
, заключенной между точками с абсциссами ![]() и
и ![]() выражается формулой
выражается формулой
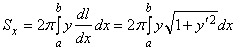 .
.
Замечание. В случае иного задания уравнения кривой площадь поверхности вращения получается из этой формулы путем соответствующей замены переменных.
2. Если кривая задана уравнениями в параметрической форме
![]() ,
, ![]() , то
, то
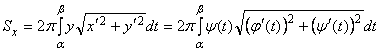 .
.
3. Если кривая определяется уравнением в полярной системе координат ![]() , то, рассматривая в зависимостях
, то, рассматривая в зависимостях ![]() полярный угол в качестве параметра, получим
полярный угол в качестве параметра, получим
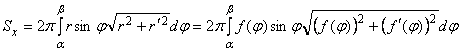 ,
,
где ![]() и
и ![]() – значения полярного угла, соответственно, начала и конца дуги.
– значения полярного угла, соответственно, начала и конца дуги.
Пример 3.13. Найти площадь поверхности, образованной вращением вокруг оси ![]() петли кривой
петли кривой ![]() (рис. 3.11).
(рис. 3.11).
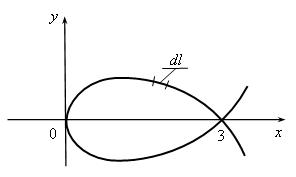
Рис. 3.11. Иллюстрация к примеру 3.13
Решение. Для верхней части кривой при ![]() имеем
имеем ![]() .
.
Отсюда ![]() . И площадь поверхности соответственно равна
. И площадь поверхности соответственно равна
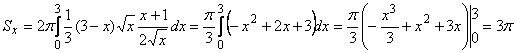 .
.
Пример 3.14. Найти площадь поверхности вращения, образованной вращением одной арки циклоиды (рис. 3.12)
![]()
вокруг ее оси симметрии.
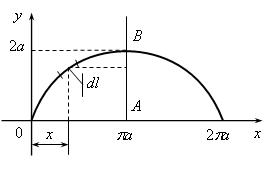
Рис. 3.12. Иллюстрация к примеру 3.14
Решение. Поверхность, площадь которой требуется найти, образована вращением дуги ОА вокруг прямой АВ, уравнение которой ![]() . Принимая в качестве независимой переменной
. Принимая в качестве независимой переменной ![]() и учитывая, что ось вращения АВ сдвинута относительно координатной оси
и учитывая, что ось вращения АВ сдвинута относительно координатной оси ![]() на расстояние
на расстояние ![]() , тогда
, тогда
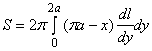 .
.
Переходя к переменной ![]() , получим
, получим
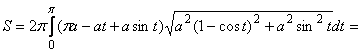
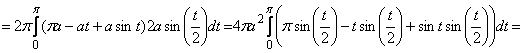
![]() .
.