Правило Лопиталя (см. разд. 2.11) применяется для раскрытия неопределенностей типа  и .

В случае неопределенности типа  или  следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности типа  или  и далее воспользоваться правилом Лопиталя. В случае неопределенности типа , , ,  следует прологарифмировать данную функцию и найти предел ее логарифма.

Пример 1. Найти .

Решение. Так как при  функции  и , то имеем неопределенность типа . Числитель и знаменатель данной дроби непрерывны, дифференцируемы и стремятся к нулю. Это означает, что можно применить правило Лопиталя:

.

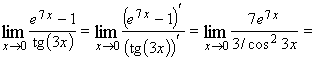
Пример 2. Найти .

Решение.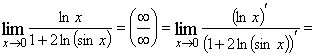           

 .

В данном случае после применения правила Лопиталя были использованы основные теоремы о пределах и первый замечательный предел.

Пример 3. Найти .

Решение.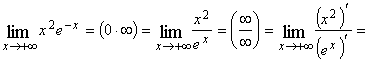       

.

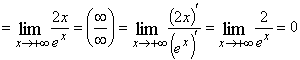Пример 4. Найти .

Решение.          

.

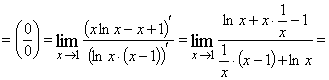
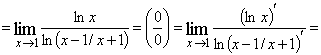
Пример 5. Найти .

Решение. В данном случае имеем неопределенность типа , поэтому для раскрытия этой неопределенности применим метод логарифмирования.

Пусть . Тогда с учетом того, что логарифмическая функция непрерывна, имеем

.

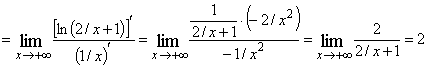Так как , то .

Пример 6. Найти .

Решение. Так как имеем неопределенность типа , то введем обозначение ,  тогда

.

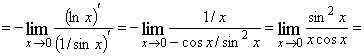
Поскольку , то .