Определение. Если функция  непрерывна при , то по определению

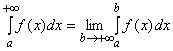.                    (3.13)

Определение. Если существует конечный предел в правой части формулы (3.13), то несобственный интеграл называется сходящимся, если этот предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

Аналогично определяется интеграл  и интеграл

.

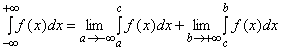Признаки сходимости и расходимости приведены только для интегралов  (3.13).

1. Если  – первообразная для функции  и существует конечный предел , то интеграл (3.13) сходится и

,

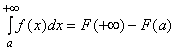если же  не существует или равен бесконечности, то интеграл (3.13) расходится.

2. Пусть при  выполняются неравенства , тогда:

если сходится интеграл 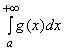, то интеграл  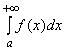тоже сходится, причем 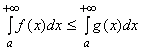; если интеграл  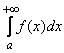расходится, то интеграл  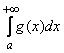тоже расходится (признак сравнения).

3. Если при   и существует конечный предел , то интегралы 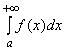 и 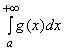 сходятся или расходятся одновременно (предельный признак сравнения).

4. Если сходится интеграл 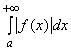, то сходится и интеграл  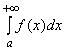(последний интеграл называется в этом случае абсолютно сходящимся).

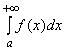5. Если при  функция  является бесконечно малой порядка  по сравнению с , то интеграл  сходится при  и расходится при .

Пример 3.19. Вычислить несобственный интеграл .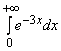

Решение.

.

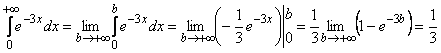Пример 3.20. Исследовать на сходимость интеграл .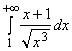

Решение. Так как для любого :

,

значит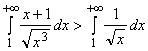   

и по признаку сравнения исследуемый интеграл расходится, так как расходится интеграл .

Пример 3.21. Исследовать на сходимость интеграл Эйлера-Пуассона

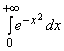.                        (3.14)

Решение. Запишем .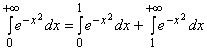

Первый из интегралов в правой части равенства не является несобственным, а второй сходится, так как для любого : 

  и  ,

следовательно, интеграл (3.14) сходится.

Пример 3.22. Исследовать на сходимость интеграл .

Решение. При  имеем:

.

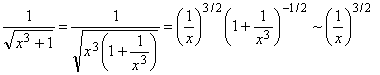Так как интеграл  сходится, то исследуемый интеграл тоже сходится.