Определение. Если функция непрерывна при  и , то по определению

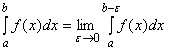.           (3.15)

Определение. Если существует конечный предел в правой части формулы (3.15), то несобственный интеграл называется сходящимся, если этот предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

Аналогично определяется несобственный интеграл в случае когда .

В случае, когда  и с – точка разрыва второго рода :

              (3.16)

Если существует непрерывная на отрезке  функция  такая, что  при  (обобщенная первообразная), то к интегралам (3.15) – (3.16) применима формула Ньютона-Лейбница

.

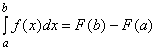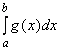Если  при  и интеграл  сходится, то интеграл (3.16) также сходится (признак сравнения).

При использовании признака сравнения чаще всего рассматривается интеграл

,

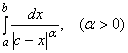который сходится при  и расходится при .

Если  и ,

т.е.  при , то при  интеграл (3.8) сходится, а при  – расходится.

Пример 3.23. Исследовать на сходимость интеграл .

Решение. Точка разрыва подынтегральной функции . Применим формулу , получим

.

Следовательно, при  будем иметь

.

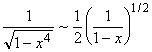Так как интеграл 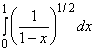 сходится, то и исследуемый интеграл тоже сходится.

Пример 3.24. Исследовать на сходимость интеграл .

Решение. При  получаем  (эквивалентная бесконечно большая), так как

.

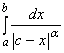Интеграл  расходится, как интеграл  при .

Следовательно, расходится и исследуемый интеграл.