Для сокращения и удобства письма в дальнейшем будем использовать следующие обозначения:

;    ;    ;    ;    .

Рассмотрим частные случаи уравнения (4.1).

Уравнение называется линейным относительно старших производных, если оно имеет вид

                     ,                            (4.2)

где  являются функциями  и . Если же эти коэффициенты зависят также и от , то уравнение называется квазилинейным.

Уравнение называется линейным, если оно линейно относительно неизвестной функции  и всех ее производных, то есть имеет вид:

                   ,                        (4.3)

где все коэффициенты функции только  и .

Если , то уравнение называется однородным, в противном случае – неоднородным.

Если все коэффициенты уравнения (4.3) постоянные, то уравнение называется линейным уравнением с постоянными коэффициентами.

С помощью взаимно-обратного преобразования переменных

                                             ,                                        (4.4)

где  дважды непрерывно дифференцируемые линейно независимые функции, можно получить новое уравнение, эквивалентное уравнению (4.2). При этом уравнение остается линейным. Конечно, преобразование будет иметь смысл, если в результате его уравнение примет более простую форму.

Используя правило дифференцирования сложной функции двух переменных, выразим производные уравнения (4.2) через новые переменные, получим:

;    ;  

;  

;  

.

Подставляя эти производные в уравнение (4.2), будем иметь:

                                             ,                                (4.5)

где

;

;  

.

Заметим, что функция  не зависит от вторых производных.

Поставим задачу: выбрать ξ и η так, чтобы в уравнении (4.5) коэффициенты  и  обратились в нуль. Для этого, как следует из выражений для этих коэффициентов, требуется найти решение уравнения с частными производными первого порядка

.                                          (4.6)

Уравнение (4.6) решается с помощью следующей леммы:

Функция  является частным решением уравнения (4.6) тогда и только тогда, когда соотношение  представляет собой общий интеграл обыкновенного дифференциального уравнения:

.                                         (4.7)

Докажем прямое утверждение. Пусть функция  удовлетворяет уравнению (4.6). Подставляя в уравнение (4.6) эту функцию, перепишем его в виде:

.                                           (*)

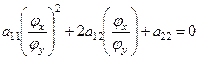Пусть функция y, определена неявным соотношением . Используем правило дифференцирования неявных функций одной переменной, получим:

.

Тогда уравнение (*) примет вид:

.

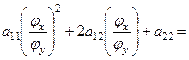
Из этого, очевидно, следует, что функция y удовлетворяет уравнению (4.7), а, значит,  – общий интеграл этого уравнения. Что и требовалось доказать. Обратное утверждение доказывается аналогично.

Уравнение (4.7) называется характеристическим для уравнения (4.3), а его интегралы – характеристиками.

Решая уравнение (1.7) как квадратное относительно , получим:

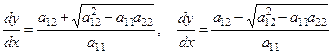.                       (4.8)

Знак подкоренного выражения определяет тип уравнения (4.2):

 – гиперболический тип;

 – эллиптический тип;

 – параболический тип.