Значительная часть задач в теории моделирования связана с построением и использованием математических моделей оптимизации. Как научное направление, теория оптимизации возникла лишь в эпоху ЭВМ, так как реализация алгоритмов поиска экстремумов чрезвычайно трудоемка, но основные методы и подходы, использующиеся в теории оптимизации, были разработаны крупнейшими математиками прошлого: Ньютоном, Эйлером, Лагранжем.
Обычная постановка задачи оптимизации состоит в следующем. В некотором n-мерном пространстве 
тем или иным способом выделяется некоторое непустое множество точек этого пространства 
, называемое допустимым множеством. Далее фиксируется некоторая вещественная функция 
, заданная во всех точках допустимого множества. Задача оптимизации состоит в том, чтобы найти точку x0 во множестве , для которой функция (целевая функция) принимает экстремальное (минимальное или максимальное) значение. Под точкой пространства понимается n-мерный вектор 
и, соответственно, 
является функцией n-мерного векторного аргумента.
Задачу оптимизации мы будем записывать следующим образом:
или 
. (4.1)
При перемене знака целевой функции все точки ее максимума превращаются, очевидно, в точки минимума и наоборот.
Следует также отметить, что термин «оптимизация функции» не вполне точно отражает существо процесса оптимизации в форме (4.1). В таком процессе сама функция остается неизменной. Речь идет об оптимизации ее значения (путем выбора соответствующей точки в допустимом n-мерном допустимом множестве значений ее аргумента .
В стандартных формах задач объектом оптимизации является непрерывная функция вещественных переменных 
, допустимая область
задается конечной системой равенств 
и неравенств с непрерывными левыми частями 
и 
. Если при этом область 
ограничена, то в ней обязательно существует, по крайней мере, одна точка абсолютного максимума и одна точка абсолютного минимума функции 
.
Поскольку перемена знака у левых частей неравенств и меняет знаки этих неравенств на противоположные, можно ограничиться одним из двух типов неравенств. Обычно при максимизации используются неравенства вида , а при минимизации – неравенства вида . Таким образом, возникают две стандартные формы постановки задач оптимизации:
(4.2)
Ограничения типа неравенств легко заменить ограничениями типа равенств и простыми координатными неравенствами, вводя дополнительные (вещественные) переменные 
. При этом ограничения вида 
заменятся парой ограничений
, 
,
а ограничения 
– парой ограничений
, .
Такой прием особенно удобно применять в тех случаях, когда по смыслу задачи все точки допустимой области имеют неотрицательные координаты. В результате его применения в таких условиях возникает третья стандартная форма постановки задачи оптимизации:
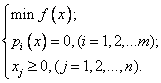(4.3)
Во всех перечисленных постановках может присутствовать дополнительное требование о том, чтобы все координаты точки оптимума были целыми числами (или числами некоторого заданного ряда). Это требование превращает задачу непрерывной оптимизации в задачу целочисленной оптимизации. В случае, когда допустимая область 
ограничена, в ней может находиться лишь конечное множество точек с
целочисленными координатами. Поэтому задача целочисленной оптимизации в ограниченной области в принципе может быть решена методом перебора, то есть путем вычисления значения целевой функции во всех допустимых точках и выбора из них точки (или точек) с оптимальными значениями критерия.