Пусть конечные точки струны закреплены, а сама струна туго натянута. Если вывести струну из положения равновесия (например, оттянуть ее или ударить по ней), то струна начнет колебаться. Будем предполагать, что все точки струны движутся перпендикулярно ее положению равновесия (поперечные колебания), причем в каждый момент времени струна лежит в одной и той же плоскости.
Введем в этой плоскости систему прямоугольных координат хОu. Тогда, если в начальный момент времени струна располагалась вдоль оси Ох, то u будет означать отклонение струны от положения равновесия. В процессе колебания величина отклонения (u)будет зависеть от абсциссы точки струны (х)и от времени (t). Таким образом, чтобы знать положение любой точки струны в произвольный момент времени, надо найти зависимость u от х и t, т. е. найти функцию ![]() .
.
При каждом фиксированном значении t график функции ![]() представляет форму колеблющейся струны в момент времени t, частная производная
представляет форму колеблющейся струны в момент времени t, частная производная ![]() даёт при этом угловой коэффициент касательной в точке с абсциссой х.
даёт при этом угловой коэффициент касательной в точке с абсциссой х.
При изменении t форма струны, очевидно, изменяется, и, чтобы представить себе процесс колебаний, мы должны построить несколько графиков функции ![]() при различных значениях t, т. е. сделать несколько мгновенных снимков колеблющейся струны.
при различных значениях t, т. е. сделать несколько мгновенных снимков колеблющейся струны.
При постоянном значении х функция ![]() дает закон движения точки с абсциссой х вдоль прямой, параллельной оси Ou, производная
дает закон движения точки с абсциссой х вдоль прямой, параллельной оси Ou, производная ![]() – скорость этого движения, а вторая производная
– скорость этого движения, а вторая производная ![]() – ускорение.
– ускорение.
Наша задача состоит в том, чтобы составить уравнение, которому должна удовлетворять функция ![]() . Для этого сделаем предварительно несколько упрощающих предположений. Будем считать струну абсолютно гибкой, т. е. не сопротивляющейся изгибу. Это означает, что если удалить часть струны, лежащую по одну сторону от какой-либо ее точки, то сила натяжения (Т), заменяющая действие удаленной части, всегда будет направлена по касательной к струне. Струна предполагается упругой и подчиняющейся закону Гука.
. Для этого сделаем предварительно несколько упрощающих предположений. Будем считать струну абсолютно гибкой, т. е. не сопротивляющейся изгибу. Это означает, что если удалить часть струны, лежащую по одну сторону от какой-либо ее точки, то сила натяжения (Т), заменяющая действие удаленной части, всегда будет направлена по касательной к струне. Струна предполагается упругой и подчиняющейся закону Гука.
Изменение величины силы натяжения при этом пропорционально изменению длины струны. Примем, что струна однородна. Линейную плотность ее обозначим буквой ρ (ρ – масса единицы длины струны).
Предположим, далее, что на струну в плоскости колебания действуют силы, параллельные оси Оu, которые могут меняться вдоль струны и со временем. Силы эти будем считать непрерывно распределенными вдоль струны. Величину силы, направленной вверх, условимся считать положительной, а силы, направленной вниз – отрицательной. Плотность распределения этих сил вдоль струны является функцией абсциссы х и времени t; обозначим ее через ![]() . Если, в частности, единственной внешней силой является вес струны, то
. Если, в частности, единственной внешней силой является вес струны, то
![]() ,
,
где ρ – плотность струны, a g – ускорение силы тяжести. Силами сопротивления среды, в которой колеблется струна, мы пока пренебрегаем.
Мы будем изучать только малые колебания струны. Если обозначить через ![]() острый угол между осью абсцисс и касательной к струне в точке с абсциссой х в момент времени t, то условие малости колебаний заключается в том, что величиной
острый угол между осью абсцисс и касательной к струне в точке с абсциссой х в момент времени t, то условие малости колебаний заключается в том, что величиной ![]() можно пренебрегать. Кроме того, так как α – малая величина, справедливы приближенные равенства:
можно пренебрегать. Кроме того, так как α – малая величина, справедливы приближенные равенства:
![]() ,
, ![]() ,
, ![]() . (4.12)
. (4.12)
Так как ![]() , то в силу полученных условий заключаем, что
, то в силу полученных условий заключаем, что ![]() .
.
Отсюда сразу следует, что в процессе колебания мы можем пренебречь изменением длины любого участка струны. Действительно, длина участка М1М2 (рис. 4.1, а) в момент времени t равна:
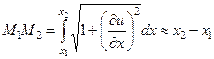 . (4.13)
. (4.13)
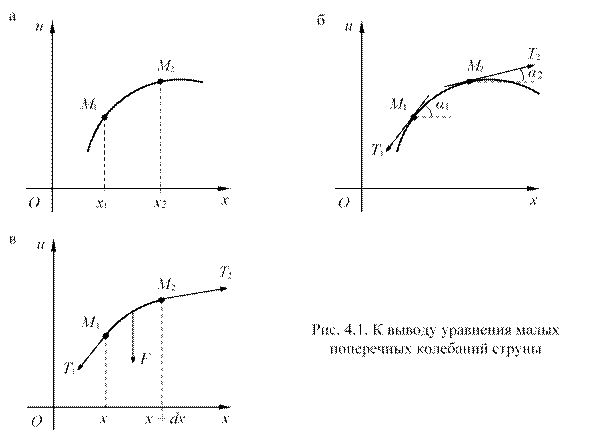 Покажем теперь, что при наших предположениях величину силы натяжения (Т)можно считать постоянной, не зависящей ни от точки ее приложения, ни от времени (t). Возьмем для этого какой-либо участок струны М1М2 (рис. 4.1, б) в момент времени t и заменим действие отброшенных участков силами натяжений T1 и Т2. Так как по условию все точки струны движутся параллельно оси Оu и внешние силы также параллельны этой оси, то сумма проекций сил натяжения на ось Ох должна равняться нулю:
Покажем теперь, что при наших предположениях величину силы натяжения (Т)можно считать постоянной, не зависящей ни от точки ее приложения, ни от времени (t). Возьмем для этого какой-либо участок струны М1М2 (рис. 4.1, б) в момент времени t и заменим действие отброшенных участков силами натяжений T1 и Т2. Так как по условию все точки струны движутся параллельно оси Оu и внешние силы также параллельны этой оси, то сумма проекций сил натяжения на ось Ох должна равняться нулю:
![]() (4.14)
(4.14)
Согласно сделанным предположениям (4.12) заключаем, что T1 = T2. Так как точки М1 и М2 выбраны произвольно, то это и доказывает, что в данный момент времени силы натяжения во всех точках равны между собой.
Поскольку мы пренебрегаем изменением длины любого участка струны, то согласно закону Гука неизменным остается и натяжение струны. Итак, мы показали, что в пределах выбранной точности Т есть величина постоянная:
Т = Т0.
Перейдем теперь к выводу уравнения колебаний струны. Выделим бесконечно малый участок струны M1M2 (рис. 4.1, в), проектирующийся в интервал ![]() оси абсцисс. На него действуют силы натяжения Т1 и Т2, заменяющие влияние отброшенных частей струны. Как уже отмечалось, силы Т1 и Т2 направлены по касательным к струне в точках М1 и М2; величина этих сил равна T0. Согласно равенству (4.14) сумма проекций сил Т1 и Т2 на ось Ох равна нулю. Вычислим сумму проекций этих же сил на ось Оu:
оси абсцисс. На него действуют силы натяжения Т1 и Т2, заменяющие влияние отброшенных частей струны. Как уже отмечалось, силы Т1 и Т2 направлены по касательным к струне в точках М1 и М2; величина этих сил равна T0. Согласно равенству (4.14) сумма проекций сил Т1 и Т2 на ось Ох равна нулю. Вычислим сумму проекций этих же сил на ось Оu:
![]() .
.
Так как
![]() ;
; ![]() ,
,
то
![]() (4.15)
(4.15)
Здесь мы заменили частное приращение производной ![]() при переходе от аргументов
при переходе от аргументов ![]() к аргументам
к аргументам ![]() её частным дифференциалом, т.е.
её частным дифференциалом, т.е. ![]() .
.
Равнодействующую внешних сил, приложенных к участку M1M2 в момент времени t, обозначим через F. Согласно определению функции ![]() и приближенному равенству (4.13) можно считать, что
и приближенному равенству (4.13) можно считать, что
![]() . (4.16)
. (4.16)
Направление равнодействующей F определится знаком функции ![]() . Направление F (см. рис. 4.1, в) соответствует случаю
. Направление F (см. рис. 4.1, в) соответствует случаю ![]() .
.
После того как найдены все силы, действующие на участок M1M2, применим второй закон Ньютона, согласно которому произведение массы на ускорение равно сумме всех действующих сил (в силу малости участка М1М2 мы рассматриваем его просто как материальную точку).
Так как масса участка M1M2 струны равна ![]() , то M1M2 =
, то M1M2 = ![]() dx. Используя формулы (4.15) и (4.16), получим:
dx. Используя формулы (4.15) и (4.16), получим:
![]() .
.
Сократив на dx и разделив все члены равенства на ![]() , приведем полученное уравнение к виду:
, приведем полученное уравнение к виду:
![]() , (4.17)
, (4.17)
где ![]() – положительная постоянная величина.
– положительная постоянная величина.
В результате мы получили линейное дифференциальное уравнение с частными производными второго порядка с постоянными коэффициентами. Уравнение (4.17) называется уравнением колебаний струны или одномерным волновым уравнением. Это одно из простейших и в то же время важнейших дифференциальных уравнений математической физики.
Если ![]() , то уравнение (4.17) называется однородным; оно описывает свободные колебания струны без воздействия внешних усилий. В противном случае уравнение называется неоднородным и описывает вынужденные колебания струны. Когда на струну действуют только силы тяжести, а натяжение струны (Т0) велико, мы вправе пренебречь вторым слагаемым в правой части уравнения струны по сравнению с первым и рассматривать, таким образом, колебания струны как свободные.
, то уравнение (4.17) называется однородным; оно описывает свободные колебания струны без воздействия внешних усилий. В противном случае уравнение называется неоднородным и описывает вынужденные колебания струны. Когда на струну действуют только силы тяжести, а натяжение струны (Т0) велико, мы вправе пренебречь вторым слагаемым в правой части уравнения струны по сравнению с первым и рассматривать, таким образом, колебания струны как свободные.