Рассмотрим задачу о колебаниях бесконечной струны. Если представить себе очень длинную струну, то ясно, что на колебания, возникшие в ее средней части, концы струны не будут оказывать заметного влияния. Так, если взять длинную натянутую веревку и слегка качнуть ее в середине, то по веревке влево и вправо побегут волны.

Картина начнет искажаться только тогда, когда волны дойдут до концов веревки и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов струны, мы, тем самым, не будем учитывать влияния отраженных волн.

Таким образом, мы приходим к задаче о свободных колебаниях неограниченной струны, которая формулируется так: решить однородное линейное дифференциальное уравнение гиперболического типа

                                                                                                               (4.18)

при начальных условиях

,                                    (4.19)

где функции  и  заданы на всей числовой оси. Никакие другие условия на искомую функцию  не накладываются. Такая задача называется задачей с начальными условиями, или задачей Коши. Метод ее решения называется методом Даламбера или методом бегущих волн.

Уравнение характеристик  распадается на два:

;        .

Характеристиками являются прямые:

;      .

Введя новые переменные , получим канонический вид уравнения колебаний:

.

Интегрируя это уравнение по , получим:

.

Интегрируя последнее уравнение по  (при фиксированном значении ), будем иметь:

.

Полученный общий интеграл запишем, подставив  и :

.                                   (4.20)

Учитывая начальные условия (4.19), получим:

,                                         (4.21)

.                                     (4.22)

Интегрируя уравнение (4.22), получим:

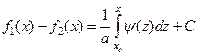.                                      (4.23)

Решая уравнение (4.23) совместно с уравнением (4.21) будем иметь:

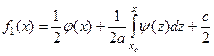 ,                                   (4.24)

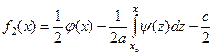.                                   (4.25)

Учитывая, что функции  и  определены для любого аргумента, заменяем x в уравнении (4.24) на  и в уравнении (4.25) на . Подставляя полученные выражения в уравнение (4.20), получим:

,

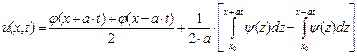или

.                              (4.26)

Выражение (4.26) называется формулой Даламбера или решением Даламбера задачи Коши для уравнения колебаний неограниченной струны. Она показывает также существование и единственность решения данной задачи.

Выясним физический смысл полученного решения. Рассмотрим два частных случая.

Пусть начальные скорости точек струны равны нулю, и струна колеблется в результате начального отклонения. В этом случае в формуле (4.26) надо положить . Тогда

.                                        (4.27)

Колебание  можно рассматривать как наложение (суперпозицию) колебаний двух волн:

· первая волна распространяется со скоростью a вправо (прямая волна);

· вторая волна  распространяется с той же скоростью влево (обратная волна).

В начальный момент времени t = 0 профили обеих волн совпадают и повторяют начальное отклонение струны с половинной амплитудой.

Пусть теперь начальное смещение , а  отлично от нуля в промежутке , а вне этого промежутка . В таком случае говорят, что струна имеет только начальный импульс (волна импульса). Тогда в соответствии с (4.26) решение имеет вид:

.                                               (4.28)

Рассмотрим функцию

.                                                 (4.29)

Используя выражение (4.29), запишем уравнение (4.28) в виде:

 .                                        (4.30)

То есть, по струне распространяются две волны импульса: прямая  и обратная , а результирующая волна  является суммой (суперпозицией) этих волн.

Вывод: действие импульса заключается в том, что с течением времени точки струны сдвигаются на отрезок, определяемый интегралом (4.28) и остаются в этом положении. Волна как бы оставляет след после своего прохождения.

Полученные результаты для колебаний бесконечной струны не могут быть применены к реальному колебанию физической струны. Действительно, при их выводе не были учтены многие факторы. В частности, опыт учит нас, что струна какой угодно длины, выведенная из положения равновесия или ударенная, колеблется. Законы колебания бесконечной струны (4.27) и (4.28) этого не показывают, потому что колебания конечной струны происходят вследствие отражения отклонений от закрепленных концов струны, а при рассмотрении бесконечной струны мы не учитываем влияния концов. Поэтому практически решения уравнений (4.27) и (4.28) применимы только для таких моментов t, для которых отклонения точек струны не успели дойти до ее концов. Кроме того, начальные функции  и  должны быть такими, чтобы в течение всего процесса  было малой величиной, которой можно пренебречь по сравнению с единицей.