Пусть на струну, закрепленную на концах, действует внешняя сила , рассчитанная на единицу длины. Чтобы исследовать колебания этой струны рассмотрим неоднородное уравнение колебаний:

 ,                                            (4.41)

в котором

,

где  – линейная плотность струны;  – плотность распределения внешних сил.

Начальные и граничные условия примут вид:

 , ,                                       (4.42)

.                                              (4.43)

Так же, как и при решении обыкновенных линейных неоднородных дифференциальных уравнений, будем искать решение уравнения (4.41) в виде суммы двух функций:

 .                                            (4.44)

Функцию  выберем так, чтобы она удовлетворяла однородному уравнению:

и условиям (4.42), (4.43).

Тогда функция  должна удовлетворять неоднородному уравнению:

,                                            (4.45)

начальным и граничным условиям:

; ;        ;        .

Легко проверить, что при таком выборе функций  и  их сумма (4.44) будет являться искомым решением.

Функция  описывает свободные колебания струны, происходящие только вследствие придания точкам струны начальных отклонений и скоростей. Функция  описывает вынужденные колебания, которые совершаются под действием внешних сил при отсутствии начальных возмущений.

Будем искать функцию  в виде ряда по собственным функциям  однородной задачи:

 ,                                          (4.46)

где  – не определенные пока функции от .

Прежде всего, заметим, что функция  действительно удовлетворяет краевым условиям , так как все собственные функции обращаются в нуль при  и .

Чтобы функция  удовлетворяла и начальным условиям, достаточно считать, что  и . Запишем уравнение (4.45) в виде:

и заменим функцию  рядом (4.46), получим:

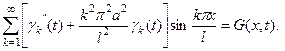                          (4.47)

Разложим теперь функцию   в интервале  в ряд по синусам по аргументу :

 ,                                           (4.48)

где

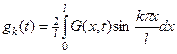                                           (4.49)

(при интегрировании  считается постоянным).

Если, в частности, плотность распределения внешних сил не зависит от времени, то функция  не зависит от , т. е.

и формула (4.48) представляет собой обычное разложение в ряд Фурье по синусам. В этом случае функции  постоянны.

Если же функция  не зависит от ,  а зависит только от времени , т.е.

,

то функции  будут равны:

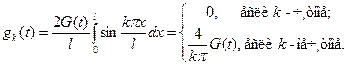                     (4.50)

Приравнивая в разложениях (4.47) и (4.48) коэффициенты при собственных функциях, составим дифференциальные уравнения для отыскания неизвестных функций :

 .                                           (4.51)

К полученному неоднородному уравнению второго порядка следует присоединить установленные ранее начальные условия:

 , .                                                  (4.52)

Составим характеристическое уравнение:

.

Решая это уравнение, получим два комплексно сопряженных корня.

Общее решение однородного уравнения, соответствующего уравнению (4.51), будет иметь вид:

где  – произвольные постоянные.

Если

,

то есть правая часть уравнения (4.51) имеет специальный вид, то частное решение можно найти методом неопределённых коэффициентов.

В случае если  – произвольная функция, то для отыскания её частного решения используют метод вариации произвольных постоянных:

;

;

.

Подставим выражение  в выражение (4.51), получим:

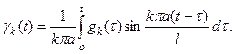                               (4.53)

После того, как все функции  найдены, остаётся подставить их в формулу (4.46), и мы получим искомую функцию.