Существует достаточно большое количество численных методов оптимизации. Классификация численных методов оптимизации:

1) по размерности решаемой задачи: одномерные и многомерные;

2) по способу формирования шага многомерные методы делятся на следующие виды:

· градиентные.

- по способу вычисления градиента – с парной пробой и с центральной пробой;

- по алгоритму коррекции шага;

- по алгоритму вычисления новой точки – одношаговые и многошаговые;

· безградиентные:

- с поочередным изменением переменных;

- с одновременным изменением переменных;

· случайного поиска:

- с чисто случайной стратегией;

- со  смешанной стратегией;

3) по наличию активных ограничений:

· без ограничений (безусловные);

· с ограничениями (условные):

- с ограничениями типа равенств;

- с ограничениями типа неравенств;

- смешанные.

Методы одномерной оптимизации являются базой для некоторых «многомерных» методов. В многомерной градиентной оптимизации строится улучшающая последовательность в зависимости от скорости изменения критерия по различным направлениям. При этом под улучшающей последовательностью понимается такая

последовательность  в каждой точке, которой значение критерия оптимальности лучше, чем в предыдущей.

В безградиентных методах величина и направление шага к оптимуму при построении улучшающей последовательности формируется однозначно по определенным детерминированным функциям в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных (т.е. градиента). Случайные методы используются в задачах высокой размерности. Многомерная условная оптимизация учитывает активные ограничения, выраженные в виде равенств и неравенств.

В каждом из рассмотренных направлений имеется большое число методов, обладающих своими достоинствами и недостатками, которые зависят, прежде всего, от свойств тех функций, экстремум которых ищется. Одним из сравнительных показателей качества метода является количество значений функции, которое нужно вычислить для решения задачи с заданной погрешностью. Чем это число меньше, тем при прочих равных условиях эффективнее метод.

Ознакомится с алгоритмами методов оптимизации можно в литературе

В настоящее время для оптимизации наиболее удобно использовать математические пакеты. Рассмотрим оптимизацию в пакете MathCAD.

Поиск минимума функции с помощью функции minerr

Рассмотрим применение функции minerr  для решения типовой оптимизационной задачи — поиск минимума. На рисунке 4.1 показано решение данной задачи градиентным методом с использованием функции minerr.

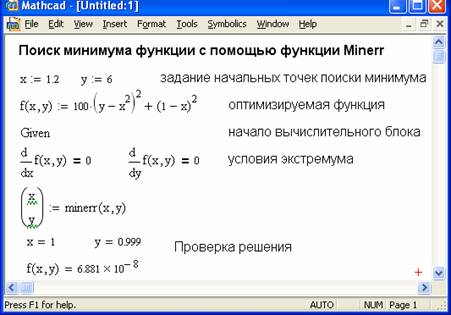
Рис. 4.1 Начало документа с решением задачи на поиск минимума функции

Нетрудно заметить, что решение данной задачи указанным методом требует вычисления производных этой функции по переменным х и у. В точке минимума эти производные равны нулю. Соответствующая реализация данного алгоритма показана на рисунке 4.1, так что не имеет смысла комментировать ее подробно.

К чести разработчиков системы Mathcad надо отметить, что данный алгоритм блестяще справляется с данной не простой задачей — минимум функции найден в точке (1;0,999) с максимально верным (в пределах точности отображения результатов вычислений) значением — 0.