Рассмотрим тонкий однородный изолированный с боков стержень конечной длины. Для выделения единственного решения уравнения теплопроводности помимо начального условия к уравнению необходимо присоединить граничные условия, которые могут быть различными в зависимости от температурного режима на границах стержня. Число различных типов граничных условий велико. В рамках данного пособия мы ограничимся рассмотрением основных, наиболее важных типов граничных условий.
Так называемая общая первая краевая задача формулируется следующим образом: найти решение ![]() уравнения теплопроводности
уравнения теплопроводности
![]() при
при ![]()
![]() , (4.86)
, (4.86)
при граничных условиях
![]() ,
, ![]() (4.87)
(4.87)
и начальном условии
![]() , (4.88)
, (4.88)
где ![]() ,
, ![]() ,
, ![]() – заданные функции.
– заданные функции.
Для начала рассмотрим частный случай этой задачи, а именно: найти решение ![]() однородного уравнения теплопроводности
однородного уравнения теплопроводности
![]() (4.89)
(4.89)
при однородных граничных условиях
![]()
![]() (4.90)
(4.90)
и при начальном условии
![]() . (4.91)
. (4.91)
Применяем метод разделения переменных Фурье, ищем частные решения уравнения (4.89) в виде:
![]() . (4.92)
. (4.92)
Подставляя u из уравнения (4.92) в уравнение (4.89), получаем два уравнения:
![]() ; (4.93)
; (4.93)
![]() . (4.94)
. (4.94)
Граничные условия (4.90) дают:
![]() ,
, ![]() . (4.95)
. (4.95)
Для нахождения нетривиальных решений уравнений (4.89) вида (4.92), удовлетворяющих граничным условиям (4.90), нужно найти нетривиальные решения уравнения (4.94), удовлетворяющие условиям (4.95).
Таким образом, для определения функции ![]() мы получили задачу о собственных значениях (задачу Штурма-Лиувилля).
мы получили задачу о собственных значениях (задачу Штурма-Лиувилля).
Рассуждая так же, как и в подразделе 4.2.3, делаем вывод, что только для значений параметра ![]() , равных
, равных
![]() (
(![]() ), (4.96)
), (4.96)
существуют нетривиальные решения уравнения (4.94), равные
![]() . (4.97)
. (4.97)
Значениям ![]() соответствуют решения уравнения (4.93):
соответствуют решения уравнения (4.93):
![]() . (4.98)
. (4.98)
Тогда функции
![]() (4.99)
(4.99)
удовлетворяют уравнению (4.89) и граничным условиям (4.90) при любых постоянных ![]() .
.
Решение уравнения (4.89), удовлетворяющее начальному условию (4.91), ищем в виде формального ряда:
![]() . (4.100)
. (4.100)
Требуя выполнения начального условия (4.91), получаем:
![]() , (4.101)
, (4.101)
где
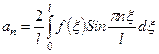 . (4.102)
. (4.102)
Нетрудно показать, что ряд (4.100) с коэффициентами ![]() , определяемыми по формуле (4.102), удовлетворяет всем условиям поставленной задачи.
, определяемыми по формуле (4.102), удовлетворяет всем условиям поставленной задачи.
Рассмотрим физический смысл полученного решения. Поступим так же, как в подразделе 4.3.3 при рассмотрении аналогичного вопроса.
Подставим уравнение (4.102) в уравнение (4.100). Опуская математические выкладки, получим:
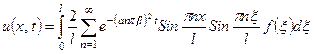 .
.
Обозначим
![]() . (4.103)
. (4.103)
Тогда функцию ![]() можно представить в виде:
можно представить в виде:
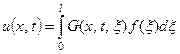 . (4.104)
. (4.104)
Можно показать, что функция ![]() , где
, где ![]() , представляет температуру стержня в любой точке (x) в фиксированный момент времени (t), вызванную действием мгновенного точечного источника мощности
, представляет температуру стержня в любой точке (x) в фиксированный момент времени (t), вызванную действием мгновенного точечного источника мощности ![]() , помещенного в момент
, помещенного в момент ![]() в точке
в точке ![]() . Эта функция называется функцией мгновенного точечного источника.
. Эта функция называется функцией мгновенного точечного источника.
Само решение (4.104) может рассматриваться как наложение функций источников, соответствующих непрерывному ряду тепловых импульсов в точках x с плотностью распределения мощностей (количеств тепла) ![]() .
.