Рассмотрим расширения определённых на множестве {0, 1} логических операций &, Ú, Ø, ® на интервал [0, 1].

Конъюнкция и дизъюнкция

Операция логического умножения обобщается следующим образом:

Функция  называется треугольной нормой, если для всех a, b, c Î [0, 1] справедливы соотношения:

1) a Ù 1 = a (1 – единица);

2) если a £ b, то a Ù c £ b Ù c (монотонность);

3) a Ù b = b Ù a (коммутативность);

4) (a Ù b) Ù с = a Ù (b Ù c) (ассоциативность).

Заметим, что, в силу неравенств 0 £  0Ùx  £  0Ù1 = 0, имеет место: 0 Ù x = 0.

Наиболее часто используются следующие треугольные нормы:

1) a Ç b = min (a, b) (Заде);

2) a * b = max(0, a + b – 1) (Лукасевич);

3) a × b = ab (произведение чисел).

Аналогично обобщается логическая сумма.

Функция  называется треугольной конормой, если для всех a, b, c Î [0, 1] справедливы соотношения:

1) 0 Ú a = a (0 – нуль);

2) если a £ b, то a Ú c £ b Ú c (монотонность);

3) a Ú b = b Ú a (коммутативность);

4) (a Ú b) Ú с = a Ú (b Ú c) (ассоциативность).

Примеры треугольных конорм:

1) a È b = max(a, b)      (Заде);

2) a Ú b = min(a + b, 1) (Лукасевич);

3) a Ú b = a + b – ab (алгебраическая сумма).

Отрицание

Наиболее общее определение функции отрицания g: [0,1] ® [0,1] предполагает, что выполнены, по крайней мере, два условия:

1) g(0) = 1;  g(1) = 0;

2) если a £ b, то g(a) ³ g(b).

Примеры отрицаний:

1)    (Заде);

2)  (квадратичное отрицание);

3)  (пороговое отрицание);

4) ,  -1 < l < ¥ (Сугено).

Две операции Ù и Ú называются g-двойственными, если

    и    .

Например, операции:

    и   

-двойственны (относительно отрицания Сугено).

Импликация

Пусть Ù – треугольная норма. Импликацией , связанной с Ù, называется такое число, что для всех x Î [0, 1] справедлива следующая эквивалентность:

x £ (a ® b), если и только если x Ù a £ b.

В силу монотонности треугольной нормы значение импликации будет равно:

a ® b = sup {x Î [0, 1] : x Ù a £ b }.

Примеры импликаций

1) Cвязанной с треугольной нормой Лукасевича будет импликация:

a ® b = min {1 – a + b, 1}.

2) C треугольной нормой заде связана импликация Гёделя:

3) C произведением a×b чисел связана импликация Гогена:

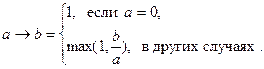
Оператор импликации не всегда связан с треугольной нормой. В частности, импликация Клини-Дайнса определяется по формуле:Øa Ú b, через операцию a Ú b = max(a,b):

a ® b = max(1-a, b).

Аналогичным образом, с помощью формулы  Øa Ú b  определяется импликация  Райхенбаха, где  a Ú b = a + b – ab сложение вероятностей:

a ® b = 1 – a + ab.

Импликация Заде аналогична последней:

a ® b = max(1 – a, min(a, b)).

Заметим, что во всех этих случаях отрицание можно определить как Øa = a ® 0.