Оптимизация режимов резания на этапе проектирования операции приводит к построению модели в форме (4.2), включающей в себя нелинейную целевую функцию и нелинейные неравенства в качестве ограничений. В качестве целевой функции наиболее часто рассматривается мера производительности обработки или мера себестоимости операции. При оптимизации по критерию производительности в качестве целевых функций могут быть использована:

функция  при работе в один проход

;        ;        = const;       > 0;   (6.2)

или функция  при работе в несколько проходов:

;      ;        = const;        > 0.   (6.3)

Очевидно, функции  и  являются мерой времени обработки. Так как  > 0 и  > 0, целевые функции в форме (6.2) и(6.3) могут быть заменены функциями в виде:

;          ;   (6.4)

;        .   (6.5)

При оптимизации по критерию себестоимости в качестве целевой функции рассматривается часть себестоимости обработки детали, которая зависит от скорости резания, подачи и глубины резания:

;       ,   (6.6)

где  – полная себестоимость работы станка и станочника (р./мин);  – время смены инструмента (мин);  – период стойкости инструмента (мин);  – время обработки резанием.

Время обработки резанием определяется следующим образом:

.   (6.7)

где  – длина обрабатываемого участка;  – припуск на обработку,  – диаметр заготовки или инструмента.

Стойкостное уравнение , как правило, представимо в следующей форме:

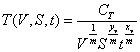.(6.8)

С учетом выражений (6.7) и (6.8), целевая функция (6.6) может быть преобразована к виду:

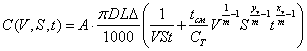; .(6.9)