Рассмотренные нами методы решения задач оптимизации применимы к широкому классу задач, однако являются весьма сложными и требуют проведения значительных объемов вычислений. Между тем существует ряд задач, являющихся частными случаями общей задачи оптимизации (4.2), для решения которых применимы методы, требующие для реализации более простых алгоритмов и значительно меньших вычислительных мощностей. К числу таких задач относится задача линейного программирования.

Задача линейного программирования сводится к поиску экстремума (максимума или минимума) линейной функции вида:

.   (7.1)

Очевидно, искать экстремум этой функции, не налагая никаких ограничений на область изменения вектора  бессмысленно, так как линейная функция не может иметь экстремума внутри допустимой области. Интерес представляет задача максимизации  при условии, что  принадлежит некоторому допустимому множеству

,   (7.2)

где  – множество допустимых значений -й переменной,  – множество индексов переменных ={1,2…}.

Те из соответствующих задач, в которых область изменения вектора  (допустимая область ) – -мерный многогранник, составляют предмет линейного программирования.

Линейным программированием называется комплекс методов оптимизации линейных функций в допустимой области, определяемой системой линейных уравнений и неравенств.

В общем случае задача линейного программирования при оптимизации функции  переменных в условиях  ограничений формулируется следующим образом:

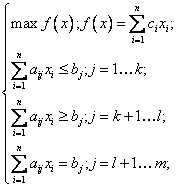           или                (7.3)

Стандартная постановка задачи линейного программирования имеет вид:

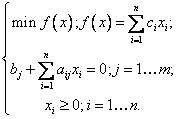   ^(7.4)

Переход от формы (7.3) к форме (7.4) осуществляется с помощью приема элиминации нетривиальных неравенств.