Практические задачи, которые приводят к построению математических моделей в форме (7.3) или (7.4), встречаются очень часто. К числу задач линейного программирования относятся ряд задач планирования производства (задача о загрузке оборудования, задача использования сырья), а также задачи оптимизации информационных, энергетических и материальных потоков в производственных системах (так называемая транспортная задача). Кроме того, методы линейного программирования применимы также для решения задачи оптимизации режимов резания, рассмотренной в разделе 5.

Для того чтобы применение методов линейного программирования к оптимизации режимов резания стало возможным, необходимо представить модель оптимизации в форме (7.3) или (7.4), то есть таким образом, чтобы нелинейная целевая функция и нелинейные ограничения были представлены линейными зависимостями. Для этого удобнее использовать модель оптимизации в форме (6.26). Процедура перехода от нелинейной степенной модели (6.26) к линейной модели (7.3) называется линеаризацией логарифмированием.

Линеаризацией называется процедура перехода от нелинейных равенств и неравенств к линейным. Линеаризация логарифмированием – процедура представления степенных (мультипликативных) зависимостей в линейной форме.

Процедура линеаризации логарифмированием позволяет произвести замену переменных и представить зависимость (6.26) в форме:

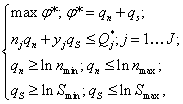   (7.5)

где , , ,  и  – показатели степени при  и  в -м ограничении (6.26), , - число функциональных ограничений в модели (6.26). Формулировка (7.5) полностью соответствует введенному нами понятию о задачах линейного программирования.

Методы решения задач линейного программирования отличаются большим разнообразием. Наиболее универсальным методом, применимым к решению широкого класса задач, является симплекс-метод. В ряде случаев целесообразно применять распределительный метод, являющийся частным случаем симплекс-метода или метод разрешающих множителей. В случае если целевая функция является функцией двух переменных, для решения задачи может быть применен графический метод решения.